
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, ta có A(x)=2x3+7x2+ax+b
=(2x3+2x2+2x)+(5x2+5x+5)+ax-7x+b-5
=2x(x2+x+1)+5(x2+x+1)+(a-7)x+(b-5)
=(x2+x+1)(2x+5)+(a-7)x+(b-5)
ta có: (x2+x+1)(2x+5)⋮B(x)
→để A(x)⋮B(x) thì (a-7)x+(b-5)=0
→\(\left\{{}\begin{matrix}a-7=0\\b-5=0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\)
vậy ....
mk trình bày hơi tắt xíu
bn cố gắng dịch nhé

1: =>x^2-5x+6-x^2-5x-6=x^2+1-x^2+9
=>-10x=10
=>x=-1(nhận)
2: \(\Leftrightarrow3x^2-15x-x^2+2x-2x^2=0\)
=>-13x=0
=>x=0
3: \(\Leftrightarrow13\left(x+3\right)+x^2-9=12x+42\)
=>x^2-9+13x+39-12x-42=0
=>x^2+x-12=0
=>(x+4)(x-3)=0
=>x=3(loại) hoặc x=-4(nhận)
4: \(\Leftrightarrow-2+x^2-5x+4=x^2+x-6\)
=>-5x-2=x-6
=>-6x=-4
=>x=2/3

\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)

a) \(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x^2+2\right)+\left(x-1\right)\left(x+1\right)-\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x}{x^2+x+1}\)


a:
DI+IE=DE
=>DE=9,5+28
=>DE=37,5
Xét ΔDEF có IK//EF
nên \(\dfrac{IK}{EF}=\dfrac{DI}{DE}\)
=>\(\dfrac{8}{x}=\dfrac{9.5}{37.5}\)
=>\(x=\dfrac{37.5\cdot8}{9.5}=\dfrac{600}{19}\)
b: Xét ΔOBA vuông tại B và ΔOCD vuông tại C có
\(\widehat{BOA}=\widehat{COD}\)
Do đó: ΔOBA đồng dạng với ΔOCD
=>\(\dfrac{AB}{CD}=\dfrac{OB}{OC}\)
=>\(\dfrac{4.2}{x}=\dfrac{3}{6}=\dfrac{1}{2}\)
=>x=8,4

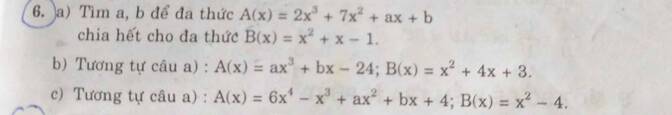


 ai giúp mik bài này đc ko ạ, mik cảm ơn!
ai giúp mik bài này đc ko ạ, mik cảm ơn!




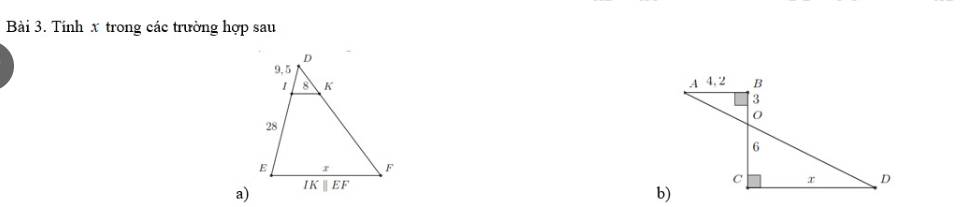 giúp mik bài này với !
giúp mik bài này với !
a: Xét ΔBDC có
M là trung điểm của BC
H là trung điểm của DC
Do đó: MH là đường trung bình của ΔBDC
Suy ra: MH//DB