K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 1 2022
a, thay x=25 vào A ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{25}}{\sqrt{25}-1}=\dfrac{5}{5-1}=\dfrac{5}{4}\)
b, \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{x\sqrt{x}-1}-\dfrac{2}{\sqrt{x}-1}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\sqrt{x^3}-1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}.\dfrac{3x+3-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
22 tháng 9 2021
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{5\sqrt{3}}{2}-9\sqrt{3}=\dfrac{5\sqrt{3}-18\sqrt{3}}{2}=\dfrac{-13\sqrt{3}}{2}\)
22 tháng 9 2021
\(=\dfrac{1}{2}.4\sqrt{3}-2.5\sqrt{3}-\sqrt{3}+5.\dfrac{\sqrt{3}}{2}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}\)
\(=-9\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{-18\sqrt{3}+5\sqrt{3}}{2}=-\dfrac{13\sqrt{3}}{2}\)
N
23 tháng 1 2022
Giải hpt:
Đặt: \(\left[{}\begin{matrix}\sqrt{x-1}=a\\y+1=b\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}3a-2b=-1\\5a-9b=-13\end{matrix}\right.< =>\left\{{}\begin{matrix}15a-10b=-5\\15a-27b=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\15a-27\cdot2=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\a=1\end{matrix}\right.\)
Thay: \(\left[{}\begin{matrix}\sqrt{x-1}=1\\y+1=2\end{matrix}\right.< =>\left[{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
13 tháng 11 2021
\(26,\\ a,\sin45^0=\cos45^0< \sin50^025'< \sin57^048'=\cos32^012'< \sin72^0=\cos18^0< \sin75^0\\ b,\tan37^026'< \tan47^0< \tan58^0=\cot32^0< \tan63^0< \tan66^019'=\cot23^041'\\ 27,\\ A=\dfrac{\left(\sin^226^0+\sin^264^0\right)+2\left(\cos^215^0+\cos^275^0\right)}{\left(\sin^255^0+\cos^255^0\right)+\left(\sin^242^0+\cos^242^0\right)}-\dfrac{\tan81^0}{2\tan81^0}\\ A=\dfrac{\left(\sin^226^0+\cos^226^0\right)+2\left(\sin^215^0+\cos^215^0\right)}{1+1}-\dfrac{1}{2}\\ A=\dfrac{1+2}{2}-\dfrac{1}{2}=2-\dfrac{1}{2}=\dfrac{3}{2}\)
\(28,\\ \sin^2\alpha=1-\cos^2\alpha=1-\dfrac{1}{2}=\dfrac{1}{2}\\ \Leftrightarrow\sin\alpha=\dfrac{\sqrt{2}}{2}\)
SE
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
\(A=\sqrt{2a\left(b+1\right)}+\sqrt{2b\left(c+1\right)}+\sqrt{2c\left(a+1\right)}\)
\(A=\dfrac{1}{\sqrt{2}}\sqrt{4a\left(b+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4b\left(c+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4c\left(a+1\right)}\)
\(A\le\dfrac{1}{2\sqrt{2}}\left(4a+b+1\right)+\dfrac{1}{2\sqrt{2}}\left(4b+c+1\right)+\dfrac{1}{2\sqrt{2}}\left(4c+a+1\right)\)
\(A\le\dfrac{1}{2\sqrt{2}}\left[5\left(a+b+c\right)+3\right]=2\sqrt{2}\)
\(A_{max}=2\sqrt{2}\) khi \(a=b=c=\dfrac{1}{3}\)
2 tháng 12 2021
\(1,\left\{{}\begin{matrix}3x-y=5\\5x+2y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+2\left(3x-5\right)=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+6x-10=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\11x=33\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3.3-5\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
\(2,\left\{{}\begin{matrix}5x-4y=3\\2x+y=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-4\left(4-2x\right)=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-16+8x=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}13x=19\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=4-2.\dfrac{19}{13}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=\dfrac{14}{13}\end{matrix}\right.\)
27 tháng 12 2021
\(b,\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\m-3\ne-3\end{matrix}\right.\Leftrightarrow m=2\\ c,\text{PT giao Ox tại hoành độ 3: }\\ x=-3;y=0\Leftrightarrow\left(m+1\right)\left(-3\right)+m-3=0\\ \Leftrightarrow-2m-6=0\Leftrightarrow m=-3\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
a.
ĐKXĐ: \(\left[{}\begin{matrix}x\ge-1+\sqrt{2}\\x\le-1-\sqrt{2}\end{matrix}\right.\)
\(x^2-2x-1+2\left(x-1\right)\sqrt{x^2+2x-1}=0\)
\(\Leftrightarrow\left(x^2+2x-1\right)+2\left(x-1\right)\sqrt{x^2+2x-1}-4x=0\)
\(\Delta'=\left(x-1\right)^2+4x=\left(x+1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+2x-1}=1-x+x+1\\\sqrt{x^2+2x-1}=1-x-x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+2x-1}=2\\\sqrt{x^2+2x-1}=-2x\left(x\le0\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+2x-1=4\\x^2+2x-1=4x^2\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow x\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
b.
ĐKXĐ: \(x\ge-\sqrt[3]{3}\)
\(x^3+3-\left(5x-1\right)\sqrt{x^3+3}+6x^2-2x=0\)
Đặt \(\sqrt{x^3+3}=t\ge0\)
\(\Rightarrow t^2-\left(5x-1\right)t+6x^2-2x=0\)
\(\Delta=\left(5x-1\right)^2-4\left(6x^2-2x\right)=\left(x-1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{5x-1-x+1}{2}=2x\\t=\dfrac{5x-1+x-1}{2}=3x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^3+3}=2x\left(x\ge0\right)\\\sqrt{x^3+3}=3x-1\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^3+2=4x^2\left(x\ge0\right)\\x^3+3=9x^2-6x+1\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)\left(x^2-3x-3\right)=0\left(x\ge0\right)\\\left(x-1\right)\left(x^2-8x-2\right)=0\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)
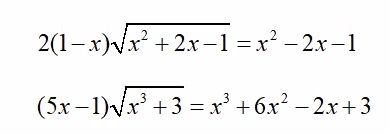
\(=\left(6\sqrt{2}-6\sqrt{2}+6\sqrt{2}\right):\sqrt{2}=6\sqrt{2}:\sqrt{2}=6\)
=(6√2−6√2+6√2):√2=6√2:√2=6