Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lim\limits_{x\rightarrow x_0}f\left(x\right)=+\infty\)

\(VT=\sqrt{\left(2+2a^2\right)\left(1+b^2\right)\left(1+c^2\right)}\)
\(VT=\sqrt{\left[a^2-2a+1+a^2+2a+1\right]\left[b^2+2bc+c^2+b^2c^2-2bc+1\right]}\)
\(VT=\sqrt{\left[\left(1-a\right)^2+\left(a+1\right)^2\right]\left[\left(bc-1\right)^2+\left(b+c\right)^2\right]}\)
Bunhiacopxki:
\(VT\ge\left(1-a\right)\left(bc-1\right)+\left(a+1\right)\left(b+c\right)=\left(1+a\right)\left(1+b\right)\left(1+c\right)-2\left(1+abc\right)\)

Ta có: \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = f'\left( {{x_0}} \right);\mathop {\lim }\limits_{x \to {x_0}} \frac{{g\left( x \right) - g\left( {{x_0}} \right)}}{{x - {x_0}}} = g'\left( {{x_0}} \right)\)
Vậy \(h'\left( {{x_0}} \right) = f'\left( {{x_0}} \right) + g'\left( {{x_0}} \right)\).

\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$

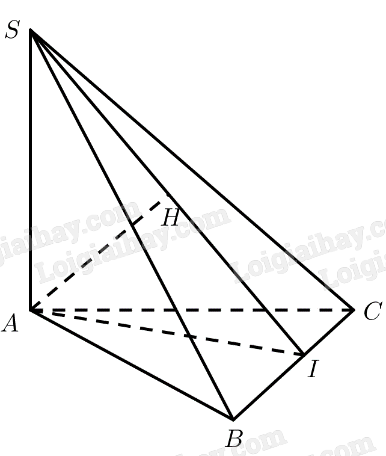
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\\AI \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAI} \right)\\\left. \begin{array}{l} \Rightarrow BC \bot AH\\AH \bot SI\end{array} \right\} \Rightarrow AH \bot \left( {SBC} \right)\end{array}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = AH\).
Lời giải:
Để hiểu công thức trên một cách đơn giản nhất thì bạn chỉ cần vẽ sơ đồ Ven ra, xác định các tập trên sẽ thấy ngay công thức trên đúng.
Nếu muốn chứng minh công thức trên theo cách minh bạch hơn thì như sau:
Trước tiên ta cm kết quả:
\(|A\cup B|=|A|+|B|-|A\cap B|\)
Thật vậy:
Đặt \(\left\{\begin{matrix} A=\left\{a_1,a_2,...,a_n, c_1,c_2,...,c_p\right\}\\ B=\left\{b_1,b_2,....,b_m,c_1,c_2,...,c_p\right\} \end{matrix}\right.\) với
\(\Rightarrow A\cup B=\left\{a_1,a_2,...,a_n, c_1,c_2,...,c_p, b_1,b_2,...,b_m\right\}\)
\(A\cap B=\left\{c_1,c_2,...,c_p\right\}\)
Ta có:
\(\Rightarrow |A|=n+p; |B|=|m+p|\); \(|A\cap B|=p; |A\cup B|=n+m+p\)
Do đó: \(|A\cup B|=|A|+|B|-|A\cap B|\)
--------------------
Áp dụng công thức trên:
\(|A\cup B\cup C|=|(A\cup B)\cup C|=|A\cup B|+|C|-|(A\cup B)\cap C|\)
\(=|A|+|B|-|A\cap B|+|C|-|(A\cap C)\cup (B\cap C)|\)
\(=|A|+|B|-|A\cap B|+|C|-(|A\cap C|+|B\cap C|)-|(A\cap C)\cap (B\cap C)|\)
\(=|A|+|B|-|A\cap B|+|C|-|A\cap C|-|B\cap C|+|A\cap B\cap C|\)
Như vậy đó.