
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 2x - 3 = 0 b) \(\dfrac{x+3}{5}\)<\(\dfrac{5-x}{3}\)
<=> 2x = 3 <=> \(\dfrac{3\left(x+3\right)}{15}< \)\(\dfrac{5\left(5-x\right)}{15}\)
<=> x = 1,5 <=> 3x + 9 < 25 - 5x
<=> 3x + 5x < 25 - 9
<=> 8x < 16
<=> x < 2
câu 2:
Gọi quãng đường AB là: x (x>0)
=> Thời gian đi từ A đến B là: x phần 25 (h)
Thời gian đi từ B đến A là : x phần 30 (h)
Vì thời gian ít hơn thời gian đi là 20 phút nên ta có pt:
20 phút = 20:60= 1 phần 3
x phần 25 -x phần 30 = 1 phần 3
tự quy đồng nhá bạn có mẫu số chung là 150 á
=> 6x-5x=50
=> x=50
vậy quãng đường AB dài : 50 km

\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)

Bài V:
-ĐKXĐ: \(x\ne\pm1\).
\(\dfrac{m}{x-1}+\dfrac{x}{x+1}=\dfrac{x^2}{x^2-1}\)
\(\Leftrightarrow\dfrac{m\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow mx+m+x^2-x=x^2\)
\(\Leftrightarrow m\left(x+1\right)=x\)
\(\Leftrightarrow m=\dfrac{x}{x+1}\)
-Vì m,x nguyên:
\(\Rightarrow x⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1-1\right)⋮\left(x+1\right)\)
\(\Rightarrow-1⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1\right)\in\left\{1;-1\right\}\)
\(\Rightarrow x\in\left\{0;-2\right\}\) (nhận)
*\(x=0\Rightarrow m=\dfrac{x}{x+1}=\dfrac{0}{0+1}=0\)
\(x=-2\Rightarrow m=\dfrac{x}{x+1}=\dfrac{-2}{-2+1}=1\)
-Vậy với \(m=0\) thì \(S=\left\{0\right\}\)
với \(m=1\) thì \(S=\left\{-2\right\}\)










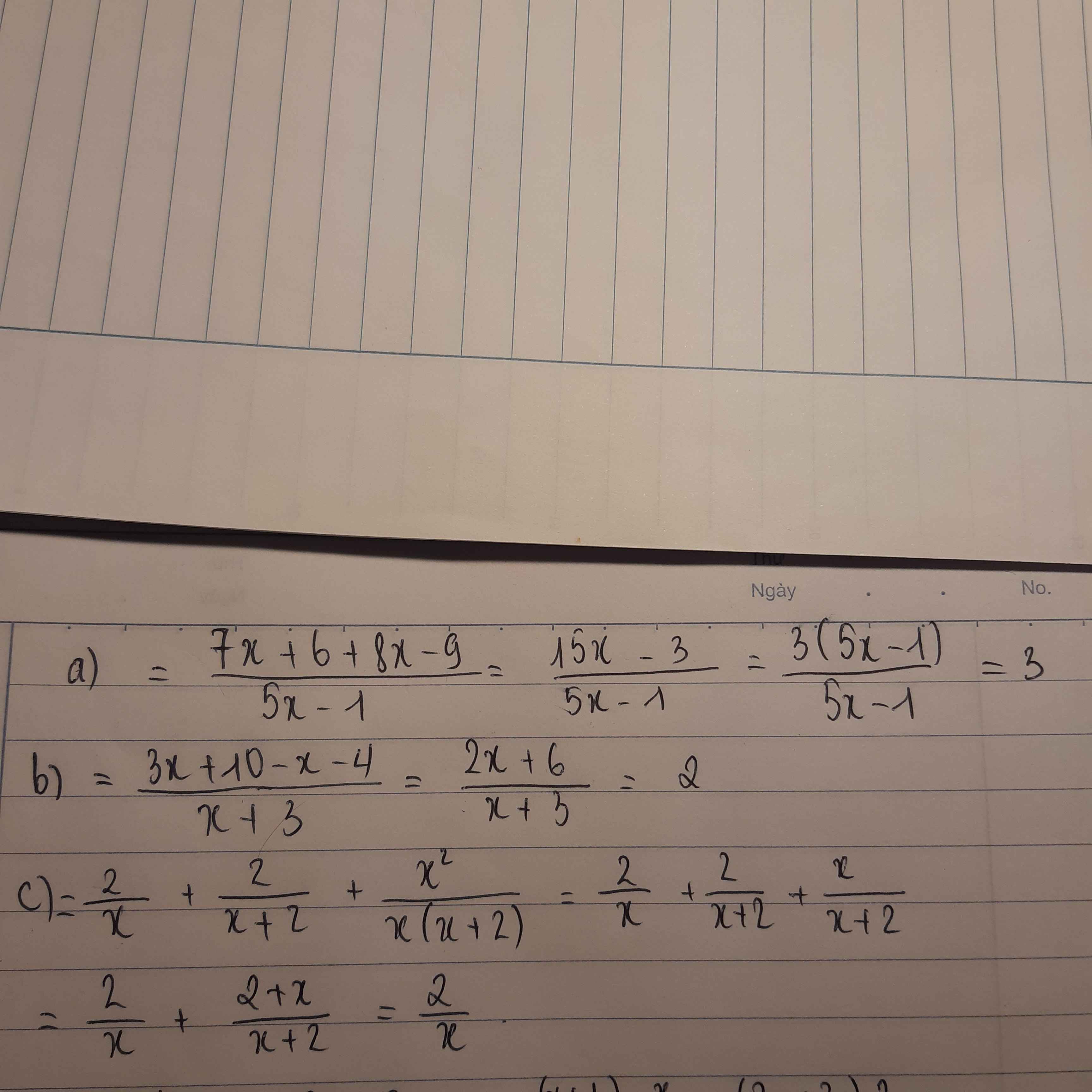
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn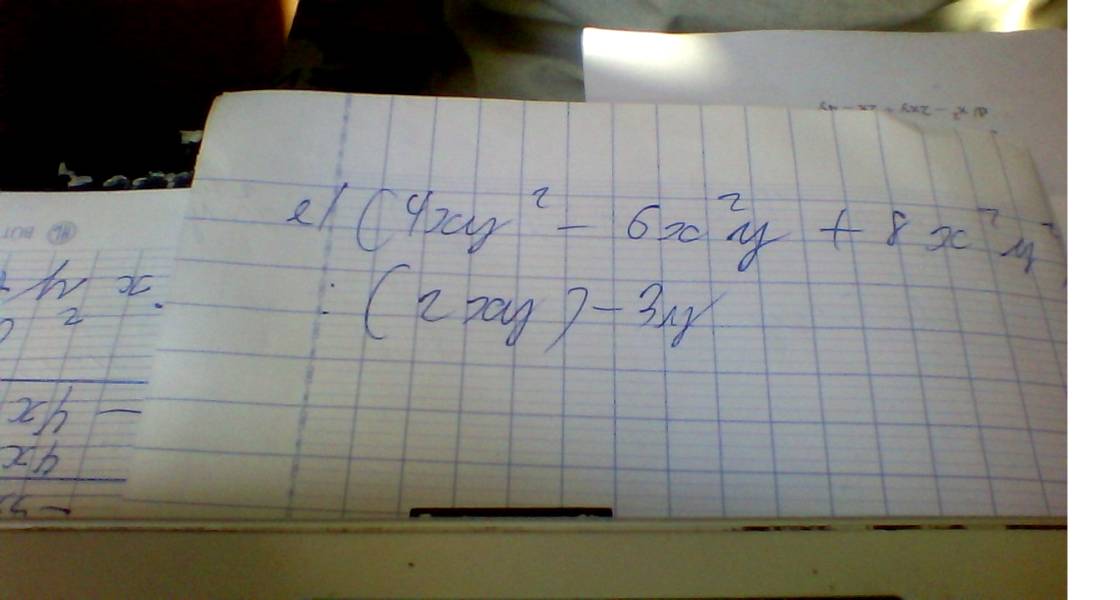
Câu 2:
Gọi số sách Nam mua được là x(sách)(Điều kiện: \(x\in Z^+\))
Số tập Nam mua được là: x+3(tập)
Theo đề, ta có phương trình:
\(12000x+5000\left(x+3\right)=83000\)
\(\Leftrightarrow12000x+5000x+15000=83000\)
\(\Leftrightarrow17000x=68000\)
hay x=4(thỏa ĐK)
Vậy: Bạn Nam mua được 4 quyển sách và 7 cuốn tập