K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 6 2023
2:
a: pi/2<a<pi
=>cosa<0
sin^2a+cos^2a=1
=>cos^2a=1-4/9=5/9
=>cosa=-căn 5/3
cos2a=2*cos^2a-1=2*5/9-1=10/9-1=1/9
sin(2a-pi/6)
=sin2a*cospi/6-cos2a*sinpi/6
=2*sina*cosa*(căn 3/2)-1/9*1/2
\(=2\cdot\dfrac{2}{3}\cdot\dfrac{-\sqrt{5}}{3}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{1}{18}=\dfrac{-4\sqrt{15}-1}{18}\)
b; tan a=2
=>sin a=2*cosa
\(A=\dfrac{3\cdot\left(2\cdot cosa\right)^2-cos^2a+2}{5\cdot\left(2\cdot cosa\right)^2+3cosa\cdot2cosa}\)
\(=\dfrac{12\cdot cos^2a-cos^2a+2}{20cos^2a+6cos^2a}\)
\(=\dfrac{11cos^2a+2\left(4cos^2a+cos^2a\right)}{26cos^2a}=\dfrac{21}{26}\)
4:
a: (C): x^2+y^2-4x+2y-4=0
=>x^2-4x+4+y^2+2y+1=9
=>(x-2)^2+(y+1)^2=9
=>I(2;-1); R=3
b: Gọi (d) là phương trình cần tìm
(d)//4x+3y-1=0
=>(d): 4x+3y+c=0
I(2;-1);R=3
Theo đề, ta có: d(I;(d))=R=3
=>\(\dfrac{\left|4\cdot2+3\cdot\left(-1\right)+c\right|}{\sqrt{4^2+3^2}}=3\)
=>|c+5|=15
=>c=10 hoặc c=-20
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
\(A=\left\{1;2;5;10;17\right\}\)
\(\left(x^2-4\right)\left(2x^2-x-1\right)=0\Rightarrow\left[{}\begin{matrix}x^2-4=0\\2x^2-x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm2\\x=1\\x=-\dfrac{1}{2}\notin Z\end{matrix}\right.\) \(\Rightarrow B=\left\{-2;1;2\right\}\)
\(\Rightarrow A\backslash B=\left\{5;10;17\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
ABC vuông cân \(\Rightarrow\left\{{}\begin{matrix}AC=AB=3\\BC=AB\sqrt{2}=3\sqrt{2}\end{matrix}\right.\)
\(\overrightarrow{BC}.\overrightarrow{CA}=-\overrightarrow{CB}.\overrightarrow{CA}=-BC.AC.cos\left(\overrightarrow{CB};\overrightarrow{CA}\right)\)
\(=-3\sqrt{2}.3.cos45^0=-9\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
I là trung điểm AB \(\Rightarrow\overrightarrow{IB}=\dfrac{1}{2}\overrightarrow{AB}\Rightarrow\overrightarrow{AB}=2\overrightarrow{IB}\)
4 tháng 1
a: E thuộc Ox nên E(x;0)
O(0;0); M(4;1); E(x;0)
\(OM=\sqrt{\left(4-0\right)^2+\left(1-0\right)^2}=\sqrt{17}\)
\(OE=\sqrt{\left(x-0\right)^2+\left(0-0\right)^2}=\sqrt{x^2}=\left|x\right|\)
Để ΔOEM cân tại O thì OE=OM
=>\(\left|x\right|=\sqrt{17}\)
=>\(x=\pm\sqrt{17}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
2.
Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)
Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)
\(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)
Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương
\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
3.
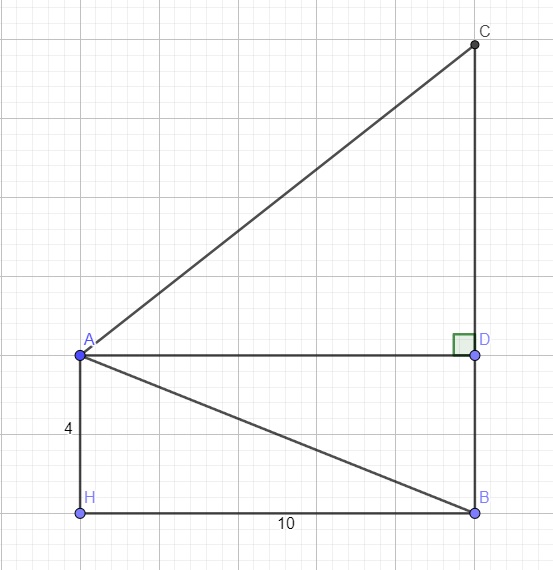
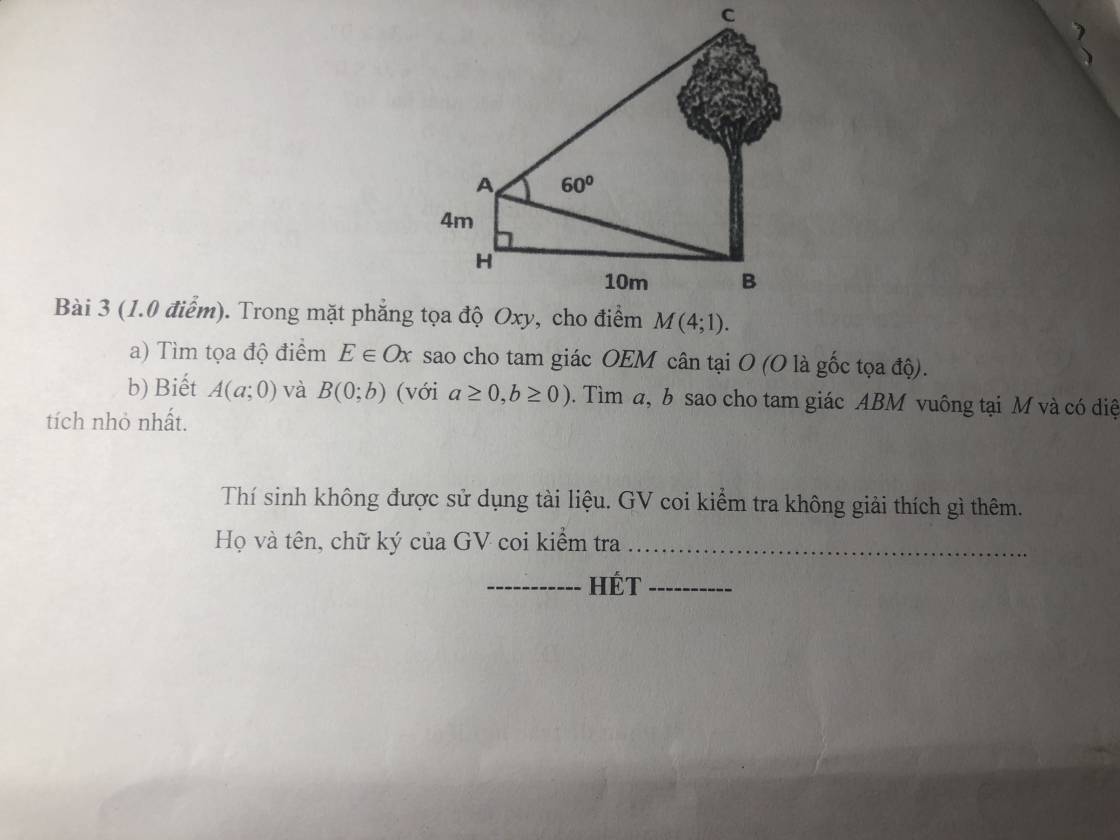
Kẻ AD vuông góc BC tại D
\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)
\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)
\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)
\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)
\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)
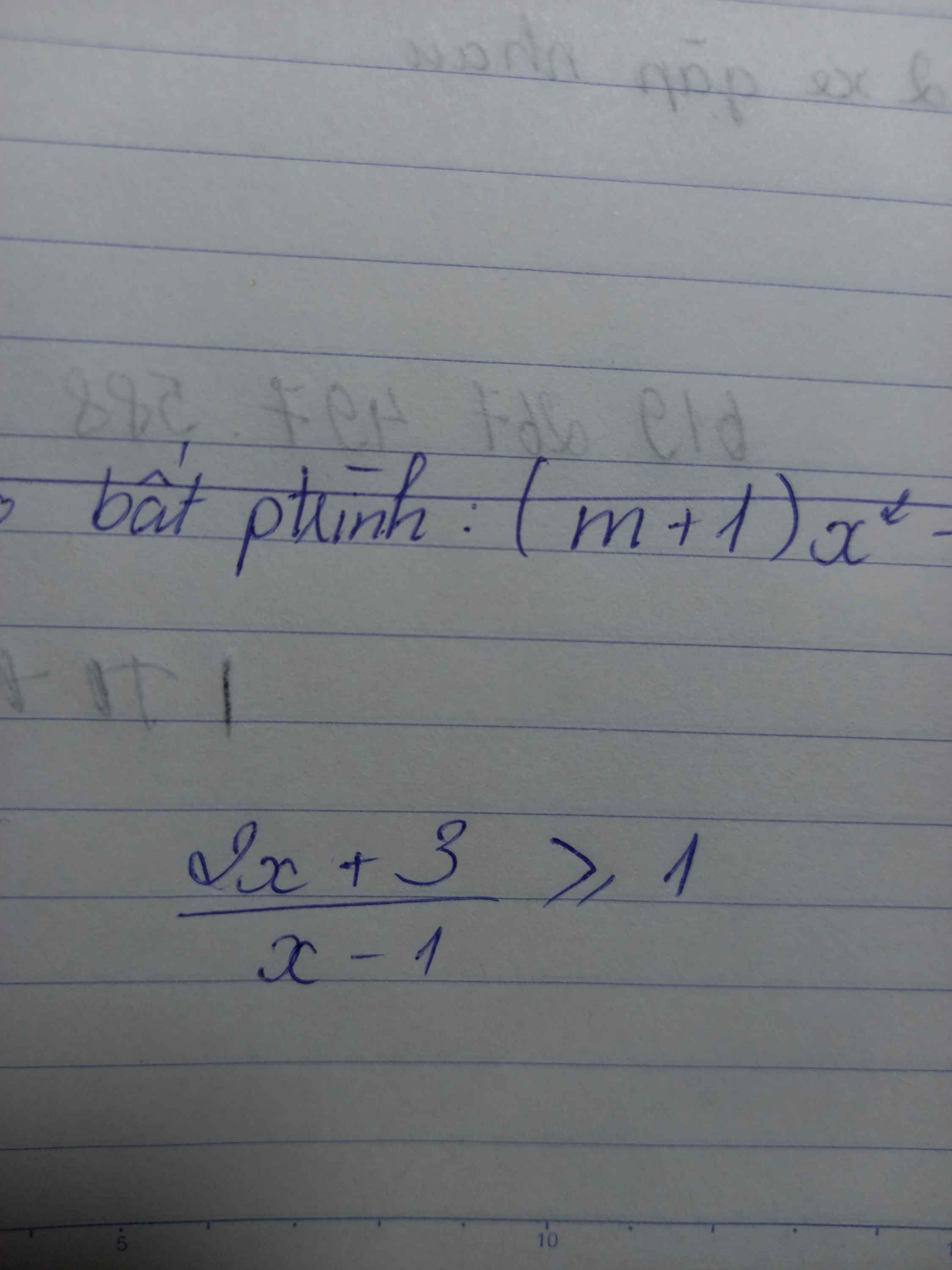
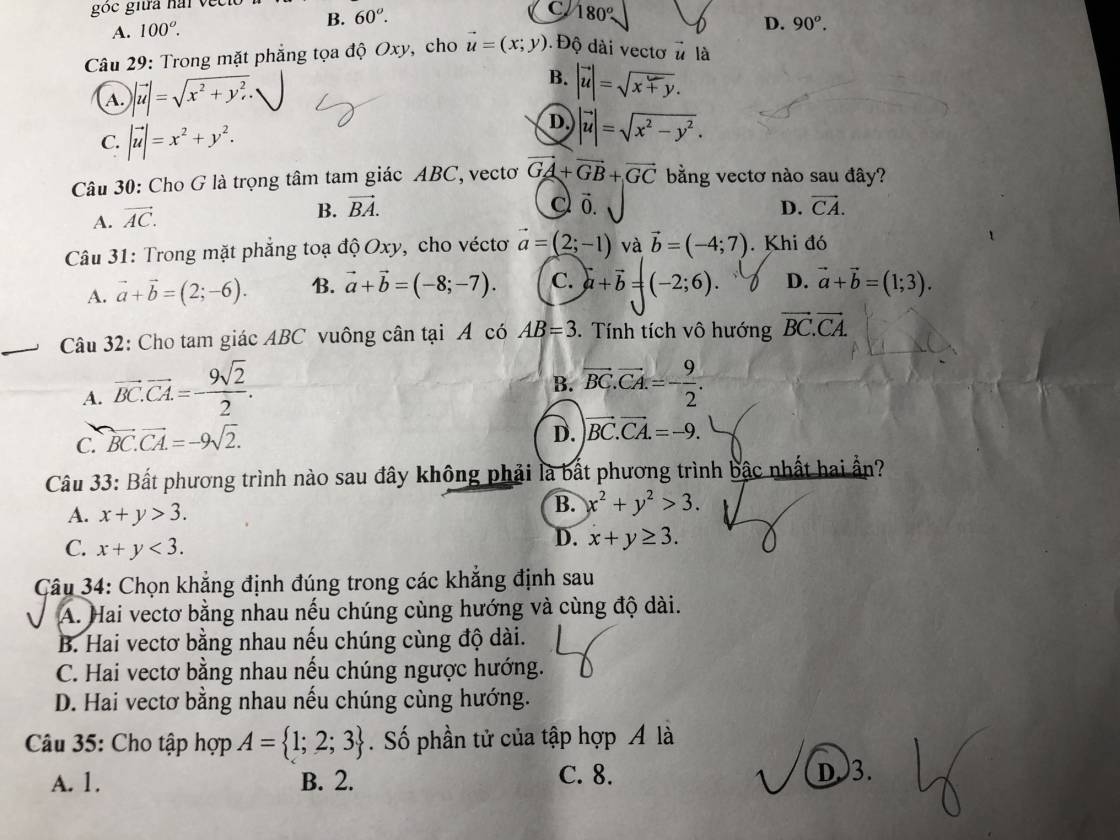
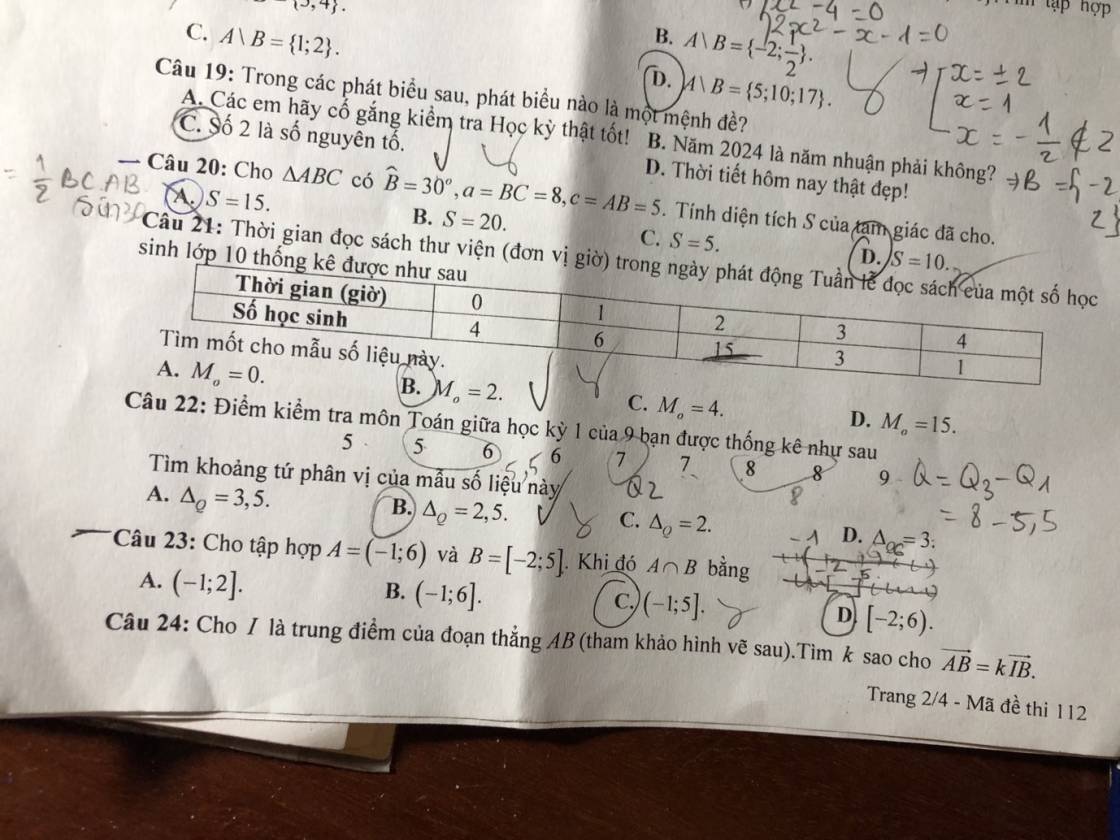
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
\(\dfrac{2x+3}{x-1}\ge1\Leftrightarrow\dfrac{2x+3}{x-1}-1\ge0\)
\(\Leftrightarrow\dfrac{x+4}{x-1}\ge0\)
\(\Rightarrow\left[{}\begin{matrix}x\le-4\\x>1\end{matrix}\right.\)