
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(x^2-9y^2=\left(x-3y\right)\left(x+3y\right)\)
c: \(\left(x+5\right)^2-16=\left(x+1\right)\left(x+9\right)\)
e: \(\left(2x+3\right)^2-\left(x-7\right)^2\)
\(=\left(2x+3+x-7\right)\left(2x+3-x+7\right)\)
\(=\left(3x-4\right)\left(x+10\right)\)


Bài 3:
a: \(M=x^2-4x+5\)
\(=x^2-4x+4+1\)
\(=\left(x-2\right)^2+1\ge1\forall x\)
Dấu '=' xảy ra khi x=2
b: \(N=y^2-y-3\)
\(=y^2-2\cdot y\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{13}{4}\)
\(=\left(y-\dfrac{1}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\forall y\)
Dấu '=' xảy ra khi \(y=\dfrac{1}{2}\)

bài 2:
a: Ta có: \(3x-2\ge7x+4\)
\(\Leftrightarrow-4x\ge6\)
hay \(x\le-\dfrac{3}{2}\)
b: Ta có: \(x+2\le6-5x^2\)
\(\Leftrightarrow5x^2+x-4\le0\)
\(\Leftrightarrow\left(x+1\right)\left(5x-4\right)\le0\)
\(\Leftrightarrow-1\le x\le\dfrac{4}{5}\)


\(a,\dfrac{11x}{2x-5}+\dfrac{x-30}{2x-5}=\dfrac{11x+x-30}{2x-5}=\dfrac{12x-30}{2x-5}=\dfrac{6\left(2x-5\right)}{2x-5}=6\)
\(b,\dfrac{3x^2-1}{2x}+\dfrac{x^2+1}{2x}=\dfrac{3x^2-1+x^2+1}{2x}=\dfrac{4x^2}{2x}=2x\)
\(c,\dfrac{3}{2x-5}+\dfrac{-2}{2x+5}+\dfrac{-20}{4x^2-25}=\dfrac{3\left(2x+5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{2\left(2x-5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{6x+15-4x+10-20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{2x+5}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{1}{2x-5}\)
\(d,\dfrac{x-2}{x-1}+\dfrac{x-3}{x+1}+\dfrac{4-2x^2}{x^2-1}=\dfrac{\left(x-2\right)\left(x+1\right)+\left(x-3\right)\left(x-1\right)+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-2x+x-2+x^2-3x-x+3+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5x+5}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5}{x-1}\)
\(e,\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}+\dfrac{4}{x^2-1}=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+2x+1-x^2+2x-1+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\)

a: Xét ΔABC vuông tại B và ΔABE vuông tại B có
AB chung
BC=BE
=>ΔABC=ΔABE
=>góc EAB=góc CAB
=>AB là phân giác của góc EAC
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>AM=AN
=>ΔAMN cân tại A
c: ΔAMH=ΔANH
=>HM=HN
mà HN<HC
nên HM<HC
e: Xét ΔAEC có
AB,CM là đường cao
AB cắt CM tại H
=>H là trực tâm
=>EH vuông góc AC
mà HN vuông góc AC
nên E,H,N thẳng hàng

\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
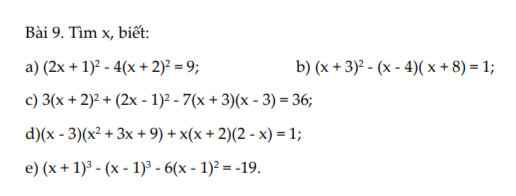



 AI GIÚP MIK VS Ạ. MAI MIK IK HỌC R Ạ
AI GIÚP MIK VS Ạ. MAI MIK IK HỌC R Ạ 
a) \(\left(2x+1\right)^2-4\left(x+2\right)^2=9\\ \Rightarrow\left(2x+1\right)^2-\left[2\left(x+2\right)\right]^2=9\\ \Rightarrow\left(2x+1-2x-4\right)\left(2x+1+2x+4\right)=9\\ \Rightarrow-3\left(4x+5\right)=9\\ \Rightarrow-12x-15=9\\ \Rightarrow x=-2\)
b) \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\\ \Rightarrow x^2+6x+9-\left(x^2+4x-32\right)=1\\ \Rightarrow x^2+6x+9-x^2-4x+32=1\\ \Rightarrow2x=-40\\ \Rightarrow x=-20\)
\(a,\Rightarrow4x^2+4x+1-4x^2-16x-16=9\\ \Rightarrow-12x=24\Rightarrow x=-2\\ b,\Rightarrow x^2+6x+9-x^2-4x+32=1\\ \Rightarrow2x=-40\Rightarrow x=-20\\ c,\Rightarrow3x^2+12x+12+4x^2-4x+1-7x^2+63=36\\ \Rightarrow8x=-40\Rightarrow x=-5\\ d,\Rightarrow x^3-27+4x-x^3=1\\ \Rightarrow4x=28\Rightarrow x=7\\ e,\Rightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6=-19\\ \Rightarrow12x=-15\Rightarrow x=-\dfrac{5}{4}\)