Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
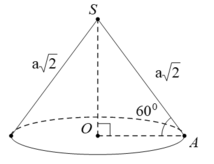
Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải thiết ta có đường sinh SA = a 2 và góc giữa đường sinh và mặt phẳng đáy là SAO ^ = 60°.


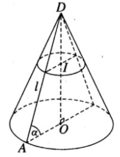
Gọi r là bán kính của đường tròn đáy.
Ta có OA = r = l.cos α (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).
Ta suy ra: S xq = πrl = πl 2 cosα
Khối nón có chiều cao h = DO = lsin α . Do đó thể tích V của khối nón được tính theo công thức
![]()
Vậy :
![]()

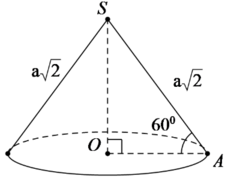
Gọi A là một điểm thuộc đường tròn đáy hình nón.
Theo giải thiết ta có đường sinh S A = a 2 và góc giữa đường sinh và mặt phẳng đáy là S A O ^ = 60 ° .
Trong tam giác vuông SAO, ta có:
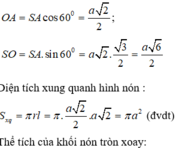
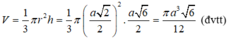

Chọn D.
(h.2.62) Gọi A là một điểm thuộc đường tròn đáy của hình nón. Dựa vào giả thiết, ta có đường sinh SA = a 2 và góc giữa đường sinh và mặt phẳng đáy là ∠ SAO = 60 °
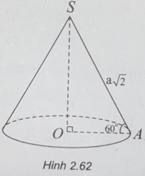
Trong tam giác vuông SAO, ta có:
OA = SA.cos60 ° = (a 2 )/2;
SO = SA.sin60 ° = (a 6 )/2.
Diện tích xung quanh hình nón:
S xq = πrl = πa 2
Thể tích của khối nón tròn xoay:
![]()

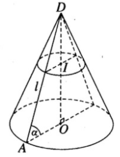
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với 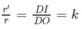
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
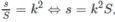
trong đó S = πr 2 = πl 2 cos 2 α
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s = k 2 s = k 2 πl 2 cos 2 α

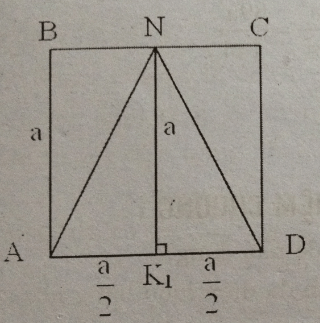
b)-Mặt phẳng (DMN) cắt hình lập phương theo thiết diện MEDNF trong đó ME // ND, FN //DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H)
-Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM.

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
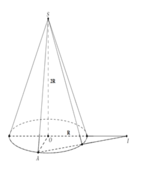
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)

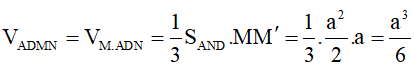

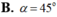

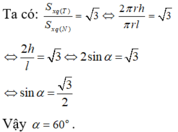
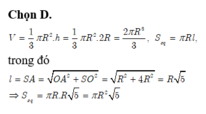
khong bt
Lấy điểm A bất kì nằm trên đường tròn đáy.
Khi đó góc tạo bởi đường sinh và mặt phẳng đáy chính là \(\widehat{SAO}=45^o\)
Do đó \(h=r=\dfrac{a}{\sqrt{2}}\)
\(\Rightarrow S_{xq}=\pi rl=\pi.\dfrac{a}{\sqrt{2}}.a=\dfrac{\pi a^2}{\sqrt{2}}\)
\(S_{tp}=S_{xq}+\pi r^2=\dfrac{\pi a^2}{\sqrt{2}}+\pi\left(\dfrac{a}{\sqrt{2}}\right)^2=\dfrac{\pi a^2\sqrt{2}+\pi a^2}{2}\)