Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\dfrac{x-5}{x-4}:\dfrac{x-5}{2x}=\dfrac{2x}{x-4}\)
\(\Rightarrow\)\(\dfrac{2x}{x-4}\in Z\)
\(\Rightarrow\)\(\dfrac{2\left(x-4\right)+8}{x-4}\in Z\)
\(\Rightarrow\)\(2+\dfrac{8}{x-4}\in Z\Rightarrow\)\(\dfrac{8}{x-4}\in Z\Rightarrow x-4\inƯ\left(8\right)=\left\{...\right\}\)
Bạn làm tiếp nhé!

\(a,P=\dfrac{2x^2+2x+2+2x-1+x^2+6x+2}{\left(x-1\right)\left(x^2+x+1\right)}\\ P=\dfrac{3x^2+10x+3}{\left(x-1\right)\left(x^2+x+1\right)}\)

a) đk: x khác 0;1
\(A=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right)\)
= \(\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left[\dfrac{\left(x+1\right)\left(x-1\right)+x+2-x^2}{x\left(x-1\right)}\right]\)
= \(\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\)
= \(\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}.\dfrac{x\left(x-1\right)}{x+1}=\dfrac{x^2}{x-1}\)
b) Để \(\left|2x-5\right|=3\)
<=> \(\left[{}\begin{matrix}2x-5=3< =>2x=8< =>x=4\left(c\right)\\2x-5=-3< =>2x=2< =>x=1\left(l\right)\end{matrix}\right.\)
Thay x = 4 vào A, ta có:
\(A=\dfrac{4^2}{4-1}=\dfrac{16}{3}\)
c) Để A = 4
<=> \(\dfrac{x^2}{x-1}=4\)
<=> \(\dfrac{x^2}{x-1}-4=0< =>\dfrac{x^2-4x+4}{x-1}=0\)
<=> \(\left(x-2\right)^2=0\)
<=> x = 2 (T/m)
d) Để A < 2
<=> \(\dfrac{x^2}{x-1}< 2< =>\dfrac{x^2}{x-1}-2< 0< =>\dfrac{x^2-2x+2}{x-1}< 0\)
<=> \(\dfrac{\left(x-1\right)^2+1}{x-1}< 0\)
Mà \(\left(x-1\right)^2+1>0\)
<=> x - 1 < 0 <=> x < 1
KHĐK: x < 1 ( x khác 0)
e) Để A thuộc Z
<=> \(\dfrac{x^2}{x-1}\in Z\)
<=> \(x^2⋮x-1\)
<=> \(x^2-x\left(x-1\right)-\left(x-1\right)⋮x-1\)
<=> \(1⋮x-1\)
Ta có bảng:
| x-1 | 1 | -1 |
| x | 2 | 0 |
| T/m | T/m |
KL: Để A thuộc Z <=> \(x\in\left\{2;0\right\}\)
f) Để A thuộc N <=> \(x\in\left\{2;0\right\}\)

Bổ sung phần c và d luôn:
c, C = \(\dfrac{2}{5}\)
\(\Leftrightarrow\) \(\dfrac{x^2-1}{2x^2+3}\) = \(\dfrac{2}{5}\)
\(\Leftrightarrow\) 5(x2 - 1) = 2(2x2 + 3)
\(\Leftrightarrow\) 5x2 - 5 = 4x2 + 6
\(\Leftrightarrow\) x2 = 11
\(\Leftrightarrow\) x2 - 11 = 0
\(\Leftrightarrow\) (x - \(\sqrt{11}\))(x + \(\sqrt{11}\)) = 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x-\sqrt{11}=0\\x+\sqrt{11}=0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x=\sqrt{11}\left(TM\right)\\x=-\sqrt{11}\left(TM\right)\end{matrix}\right.\)
d, Ta có: \(\dfrac{x^2-1}{2x^2+3}\) = \(\dfrac{x^2+\dfrac{3}{2}-\dfrac{5}{2}}{2\left(x^2+\dfrac{3}{2}\right)}\) = \(\dfrac{1}{2}\) - \(\dfrac{5}{4\left(x^2+\dfrac{3}{2}\right)}\)
C nguyên \(\Leftrightarrow\) \(\dfrac{5}{4\left(x^2+\dfrac{3}{2}\right)}\) nguyên \(\Leftrightarrow\) 5 \(⋮\) 4(x2 + \(\dfrac{3}{2}\))
\(\Leftrightarrow\) 4(x2 + \(\dfrac{3}{2}\)) \(\in\) Ư(5)
Xét các TH:
4(x2 + \(\dfrac{3}{2}\)) = 5 \(\Leftrightarrow\) x2 = \(\dfrac{-1}{4}\) \(\Leftrightarrow\) x2 + \(\dfrac{1}{4}\) = 0 (Vô nghiệm)
4(x2 + \(\dfrac{3}{2}\)) = -5 \(\Leftrightarrow\) x2 = \(\dfrac{-11}{4}\) \(\Leftrightarrow\) x2 + \(\dfrac{11}{4}\) = 0 (Vô nghiệm)
4(x2 + \(\dfrac{3}{2}\)) = 1 \(\Leftrightarrow\) x2 = \(\dfrac{-5}{4}\) \(\Leftrightarrow\) x2 + \(\dfrac{5}{4}\) = 0 (Vô nghiệm)
4(x2 + \(\dfrac{3}{2}\)) = -1 \(\Leftrightarrow\) x2 = \(\dfrac{-7}{4}\) \(\Leftrightarrow\) x2 + \(\dfrac{7}{4}\) = 0 (Vô nghiệm)
Vậy không có giá trị nào của x \(\in\) Z thỏa mãn C \(\in\) Z
Chúc bn học tốt! (Ko bt đề sai hay ko nữa :v)

\(A=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right)\cdot\dfrac{x^2\left(2-x\right)}{4x\left(x-3\right)}\)
\(=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{4\left(x-3\right)}\)
\(=\dfrac{-4x^2-8x}{x+2}\cdot\dfrac{-x}{4\left(x-3\right)}=\dfrac{-4x\left(x+2\right)}{\left(x+2\right)}\cdot\dfrac{-x}{4\left(x-3\right)}\)
\(=\dfrac{x^2}{x-3}\)

a, Để B xác định
\(\Leftrightarrow\left\{{}\begin{matrix}x-2\ne0\\x+2\ne0\\4-x^2\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-2\end{matrix}\right.\)
\(b,B=\dfrac{3}{x-2}+\dfrac{-2}{x+2}-\dfrac{x-14}{4-x^2}\)
\(=\dfrac{3\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{-2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{x-14}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{3x+6-2x+4+x-14}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2}{x+2}\)
c, Đẻ B có giá trị nguyên
\(\Leftrightarrow2⋮x+2\Leftrightarrow x+2\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)
Ta có bẳng sau:
| \(x+2\) | 1 | -1 | 2 | -2 |
| 2 | -1 | -3 | 0 | -4 |
Vậy \(x\in\left\{-1;-3;0;-4\right\}\) thì B có giá trị nguyên

Để A nguyên thì x^2 chia hết cho x+1
=>x^2-1+1 chia hết cho x+1
=>\(x+1\in\left\{1;-1\right\}\)
=>\(x\in\left\{0;-2\right\}\)

a: \(A=\dfrac{x^2-2x+2x^2+4x-3x^2-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2}{x+2}\)
a, \(\dfrac{x}{x+2}\) + \(\dfrac{2x}{x-2}\) -\(\dfrac{3x^2-4}{x^2-4}\)
= \(\dfrac{x}{x+2}+\dfrac{2x}{x-2}-\dfrac{3x^2+4}{x^2-4}\)
= \(\dfrac{x}{x+2}+\dfrac{2x}{x-2}-\dfrac{3x^2+4}{\left(x+2\right)\left(x-2\right)}\)
= \(\dfrac{x\left(x-2\right)+2x\left(x+2\right)-3x^2-4}{\left(x+2\right)\left(x-2\right)}\)
= \(\dfrac{2x-4}{\left(x+2\right)\left(x-2\right)}=\dfrac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{2}{x+2}\)
Có vài bước mình làm tắc á nha :>
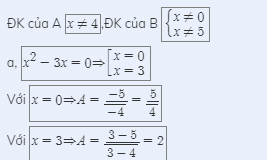

b: \(B=\dfrac{2x-8+x+20}{\left(x+4\right)\left(x-4\right)}=\dfrac{3x+12}{\left(x+4\right)\left(x-4\right)}=\dfrac{3}{x-4}\)