Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A=1-\(\dfrac{1}{2^2}\)-\(\dfrac{1}{3^2}\)-...-\(\dfrac{1}{2022^2}\) Chứng minh A>\(\dfrac{1}{2022}\)

A=1-(1/2^2+1/3^2+...+1/2022^2)
1/2^2+1/3^2+...+1/2022^2<1/1*2+1/2*3+...+1/2021*2022=1-1/2022=2021/2022
=>-(1/2^2+...+1/2022^2)>-2021/2022
=>A>1/2022

vì: \(\dfrac{1}{4^2}< \dfrac{1}{4}\)
\(\dfrac{1}{6^2}< \dfrac{1}{4}\)
........
\(\dfrac{1}{2020^2}< \dfrac{1}{4}\)
=> \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+.......+\dfrac{1}{2020^2}< \dfrac{1}{4}\)

\(B=\left(\dfrac{2020}{2}+1\right)+\left(\dfrac{2019}{3}+1\right)+...+\left(\dfrac{1}{2021}+1\right)+1\)
\(=\dfrac{2022}{2}+\dfrac{2022}{3}+...+\dfrac{2022}{2021}+\dfrac{2022}{2022}\)
=2022(1/2+1/3+...+1/2021+1/2022)
=>B/A=2022

(\(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2023}\)). x = (\(\dfrac{2021}{2}+1\))+(\(\dfrac{2020}{3}+1\))+....+(\(\dfrac{1}{2022}+1\))
(\(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2023}\)). x = \(\dfrac{2023}{2}\)+\(\dfrac{2023}{3}\)+....+ \(\dfrac{2023}{2022}\)
(\(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2023}\)). x = 2023.( \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2023}\))
vậy x= 2023

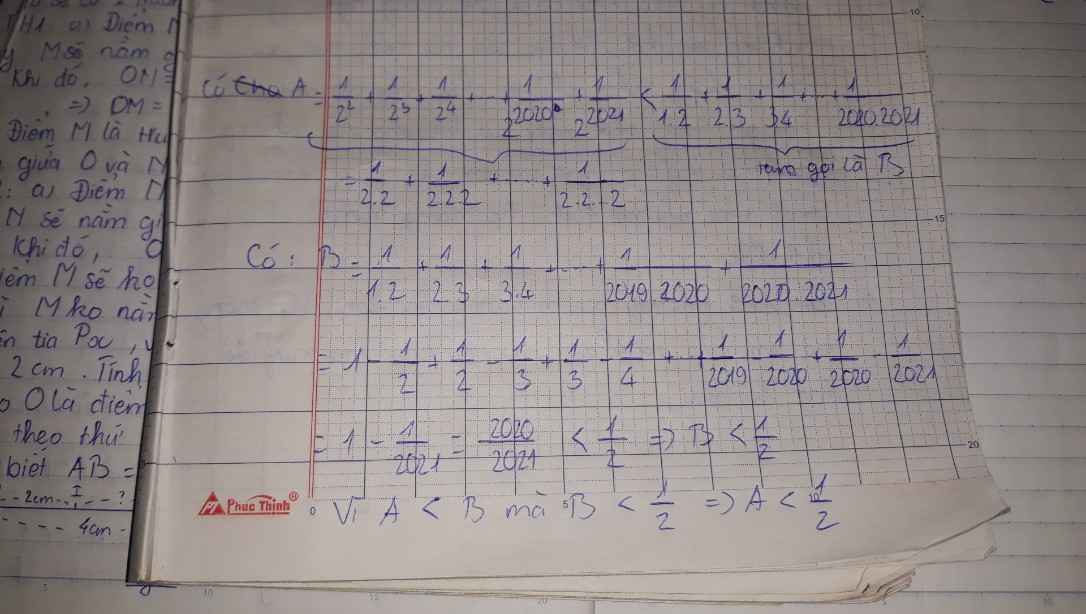
Ta có: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2021.2022}\)
\(\Rightarrow A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(\Rightarrow A< 1-\dfrac{1}{2022}< 1\left(đpcm\right)\)

làm vào bài đừng có dùng ngoặc kép như tui nha,tui làm minh họa cho bạn hiểu
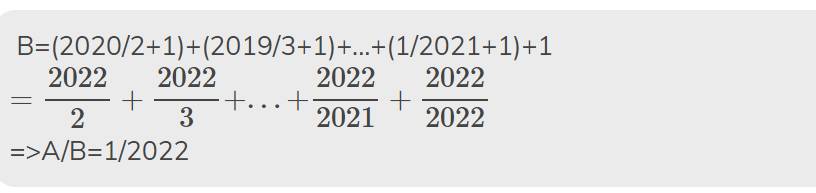

4A=1-1/2^2+1/2^4-...+1/2^2018-1/2^2020
=>5A=1-1/2^2022
=>A=1/5-1/5*2^2022<1/5=0,2