Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) ta có: A= x^3 -8y^3=> A=(x-2y)(x^2 +2xy+4y^2)=>A=5.(29+2xy) (vì x-2y=5 và x^2+4y^2=29) (1)
Mặt khác : x-2y=5(gt)=> (x-2y)^2=25=> x^2-4xy+4y^2=25=>29-4xy=25(vì x^2+4y^2=29)
=> xy=1 (2)
Thay (2) vào (1) ta đc: A= 5.(29+2.1)=155
Vậy gt của bt A là 155
2) theo bài ra ta có: a+b+c=0 => a+b=-c=>(a+b)^2=c^2=> a^2 +b^2+2ab=c^2=>c^2-a^2-b^2=2ab
=> \(\left(c^2-a^2-b^2\right)^2=4a^2b^2\)
=>\(c^4+a^4+b^4-2c^2a^2+2a^2b^2-2b^2c^2=4a^2b^2\)
=>\(a^4+b^4+c^4=2a^2b^2+2b^2c^2+2c^2a^2\)
=>\(2\left(a^4+b^4+c^4\right)=\left(a^2+b^2+c^2\right)^2\)
=> \(a^4+b^4+c^4=\frac{1}{2}\left(a^2+b^2+c^2\right)^2\) (đpcm)

Giả sử : \(y=ax\)
Thay vào giả thiết : \(\frac{ax}{x+ax}+\frac{2\left(ax\right)^2}{x^2+\left(ax\right)^2}+\frac{4\left(ax\right)^4}{x^4+\left(ax\right)^4}+\frac{8\left(ax\right)^8}{x^8-\left(ax\right)^8}=4\)
\(\Leftrightarrow\frac{x.a}{x.\left(a+1\right)}+\frac{x^2.2a^2}{x^2\left(1+a^2\right)}+\frac{x^4.4a^4}{x^4\left(1+a^4\right)}+\frac{x^8.8a^8}{x^8\left(1-a^8\right)}=4\)
\(\Leftrightarrow\frac{a}{a+1}+\frac{2a^2}{a^2+1}+\frac{4a^4}{a^4+1}+\frac{8a^8}{1-a^8}=4\)
Tới đây bạn giải ra , tìm a rồi thay vào y = ax là ra :)

Từ x8+x4y4+y8=(x4+y4)2-x4y4=(x4+y4-x2y2) (x4+y4+x2y2)=4(x4+y4-x2y2) =8
=>(x4+y4-x2y2)=2=>x4+y4=2+x2y2 kết hợp với x4+y4+x2y2=4
=> 2+x2y2+x2y2=4 => x2y2=1 (x4y4 sẽ = 1 nốt ) => x4+y4=3 và x8+y8=7
Xét (x4+y4)3=x12+y12+3x4y4(x4+y4)=x12+y12+3.1.3=33=27
=>x12+y12=18=> A = 18+1=19

Bài 2:
\(A=\left(x+y\right)^3-3xy\left(x+y\right)+3xy=1^3-3xy+3xy=1\)
Bài 3:
\(M=x^6-x^4-x^4+x^2+x^3-x\)
\(=x^3\left(x^3-x\right)-x\left(x^3-x\right)+\left(x^3-x\right)\)
\(=8x^3-8x+8\)
\(=8\cdot8+8=72\)
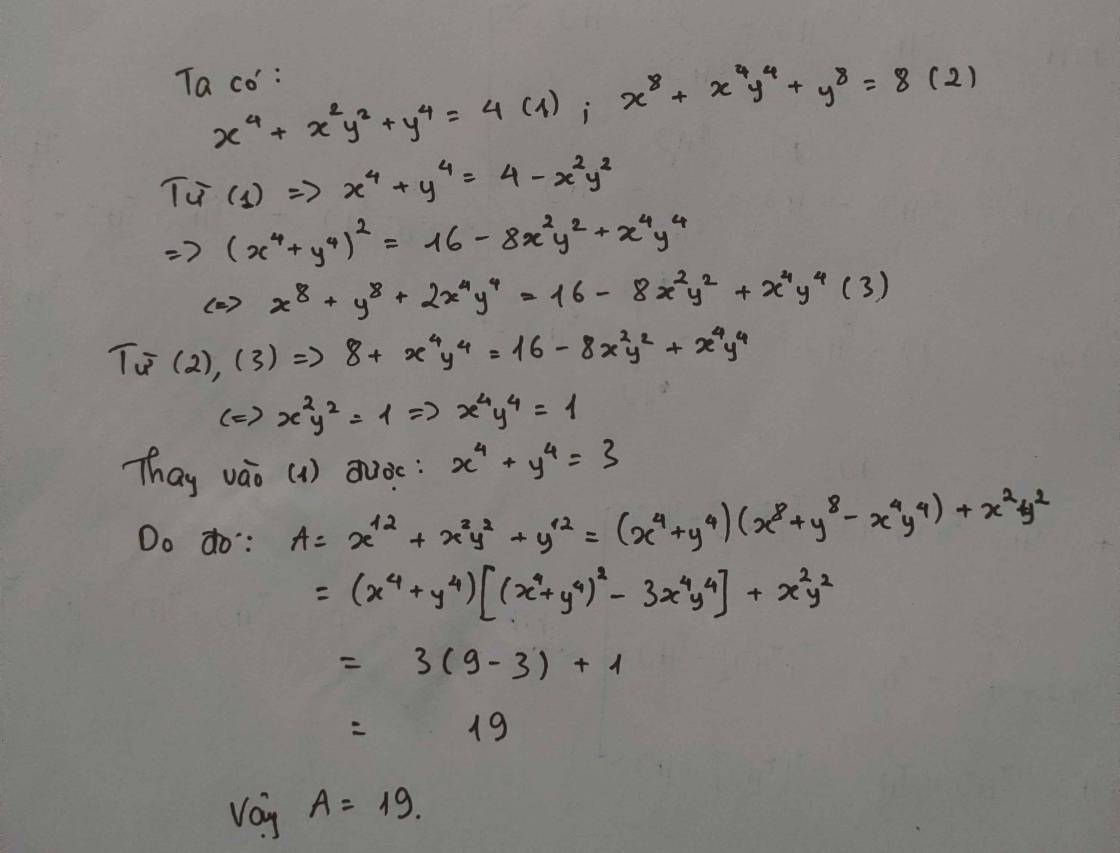
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn. Viết đề như trên khó theo dõi quá.