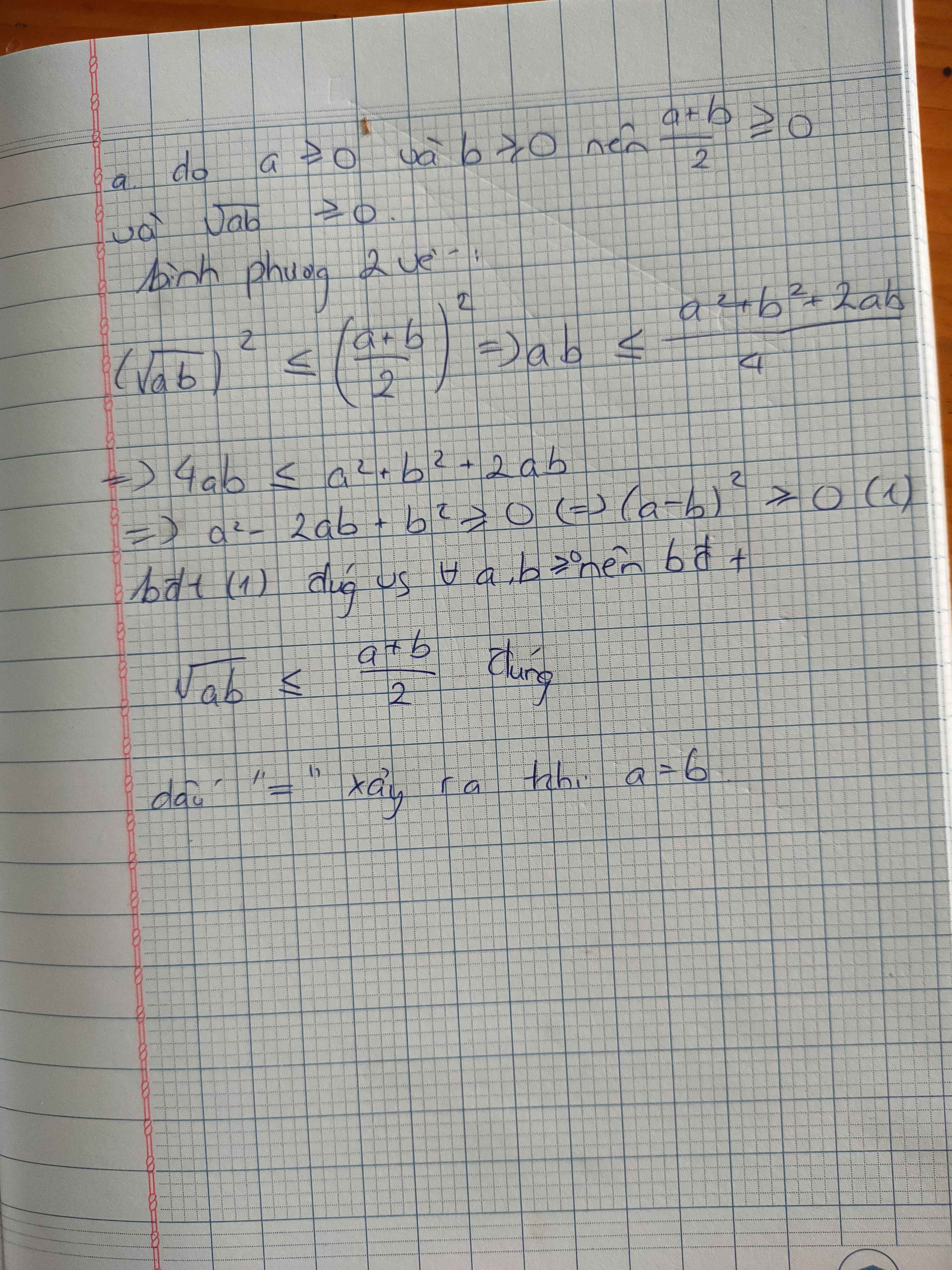K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
R
18 tháng 2 2022
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
15 tháng 2 2016
ôi dào !dễ ợt ! cô em mới cho học ngày hôm qua !k đi rùi em trình bày cho cách làm !
KA
1
28 tháng 6 2021
`sqrta+1>sqrt{a+1}`
`<=>a+2sqrta+1>a+1`
`<=>2sqrta>0`
`<=>sqrta>0AAa>0`
`sqrt{a-1}<sqrta`
`<=>a-1<a`
`<=>-1<0` luôn đúng
`sqrt6-1>sqrt3-sqrt2`
`<=>sqrt6-sqrt3+sqrt2-1>0`
`<=>sqrt3(sqrt2-1)+sqrt2-1>0`
`<=>(sqrt2-1)(sqrt3+1)>0` luôn đúng
2 tháng 9 2016
Ta có 15P = 3a5b \(\le\)\(\frac{9a^2+25b^2}{2}\)
= \(\frac{\left(3a+5b\right)^2-30ab}{2}\)
=> 30P \(\le\)\(\frac{12^2}{2}\)
=> P \(\le\)\(\frac{12}{5}\)
Đạt được khi a = 2; b = \(\frac{6}{5}\)
OI
3
13 tháng 8 2017
3) Đặt b+c=x;c+a=y;a+b=z.
=>a=(y+z-x)/2 ; b=(x+z-y)/2 ; c=(x+y-z)/2
BĐT cần CM <=> \(\frac{y+z-x}{2x}+\frac{x+z-y}{2y}+\frac{x+y-z}{2z}\ge\frac{3}{2}\)
VT=\(\frac{1}{2}\left(\frac{y}{x}+\frac{z}{x}-1+\frac{x}{y}+\frac{z}{y}-1+\frac{x}{z}+\frac{y}{z}-1\right)\)
\(=\frac{1}{2}\left[\left(\frac{x}{y}+\frac{y}{x}\right)+\left(\frac{y}{z}+\frac{z}{y}\right)+\left(\frac{x}{z}+\frac{z}{x}\right)-3\right]\)
\(\ge\frac{1}{2}\left(2+2+2-3\right)=\frac{3}{2}\)(Cauchy)
Dấu''='' tự giải ra nhá
13 tháng 8 2017
Bài 4
dễ chứng minh \(\left(a+b\right)^2\ge4ab;\left(b+c\right)^2\ge4bc;\left(a+c\right)^2\ge4ac\)
\(\Rightarrow\left(a+b\right)^2\left(b+c\right)^2\left(a+c\right)^2\ge64a^2b^2c^2\)
rồi khai căn ra \(\Rightarrow\)dpcm.
đấu " = " xảy ra \(\Leftrightarrow\)\(a=b=c\)
AH
Akai Haruma
Giáo viên
17 tháng 9 2023
Lời giải:
CM $\sqrt{a}+\sqrt{b}> \sqrt{a+b}$
BĐT cần chứng minh tương đương với:
$(\sqrt{a}+\sqrt{b})^2> a+b$
$\Leftrightarrow a+b+2\sqrt{ab}> a+b$
$\Leftrightarrow \sqrt{ab}>0$ (luôn đúng với mọi $a>0, b>0$)
Ta có đpcm
--------------------
CM $|a|+|b|> |a+b|$. Cái này là = rồi chứ không phải > bạn nhé.
Khi $a>0; b>0$ thì $|a|=a; |b|=b\Rightarrow |a|+|b|=a+b$
$|a+b|=a+b$
$\Rightarrow |a|+|b|=|a+b|$
22 tháng 11 2021
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\Leftrightarrow ab+bc+ca=0\)
Cần cm:
\(\sqrt{a+b}=\sqrt{a+c}+\sqrt{b+c}\\ \Leftrightarrow a+b=a+b+2c+2\sqrt{\left(a+c\right)\left(b+c\right)}\\ \Leftrightarrow2c+2\sqrt{ab+ac+bc+c^2}=0\\ \Leftrightarrow2c+2\sqrt{c^2}=0\\ \Leftrightarrow2c+2\left|c\right|=0\\ \Leftrightarrow2c-2c=0\left(c< 0\right)\\ \Leftrightarrow0=0\left(luôn.đúng\right)\)
Vậy đẳng thức đc cm
KN
1
26 tháng 9 2021
Bài 1:
Ta có: \(a+b\ge2\sqrt{ab}\)
\(b+c\ge2\sqrt{bc}\)
\(a+c\ge2\sqrt{ac}\)
Do đó: \(2\left(a+b+c\right)\ge2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\)
hay \(a+b+c\ge\sqrt{ab}+\sqrt{cb}+\sqrt{ac}\)