Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gặp những bài cần tính toán thế này làm biếng lắm, dựng hình thì dễ chứ tính thì chả muốn tính chút xíu nào.
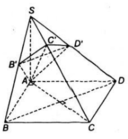
Trong mp đáy, kéo dài AD và BC cắt nhau tại E \(\Rightarrow D\) là trung điểm AE (đường trung bình) \(\Rightarrow AE=AB=2a\)
Ta có: \(\left\{{}\begin{matrix}AD\perp AB\\SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD\perp SB\)
\(\Rightarrow AD\in\left(\alpha\right)\)
Trong mp (SAB), kẻ \(AM\perp SB\Rightarrow M\in\left(\alpha\right)\)
Dễ dàng chứng minh tam giác ACB vuông cân tại C (Pitago đảo) \(\Rightarrow BC\perp\left(SAC\right)\)
Trong mp (SAC), kẻ \(AN\perp SC\Rightarrow AN\perp\left(SBC\right)\Rightarrow AN\perp SB\Rightarrow N\in\left(\alpha\right)\)
\(\Rightarrow\) Thiết diện là tứ giác AMND
\(SB=SE=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(AM=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{2a\sqrt{5}}{5}\)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{AC^2+SA^2}=a\sqrt{3}\)
\(CN=\dfrac{AC^2}{SC}=\dfrac{2a\sqrt{3}}{3}\) ; \(EC=BC=a\sqrt{2}\Rightarrow EN=\sqrt{EC^2+CN^2}=\dfrac{a\sqrt{30}}{3}\)
\(DE=AD=a\)
\(S_{AME}=\dfrac{1}{2}AM.AE=...\)
\(S_{DNE}=\dfrac{1}{2}DE.EN.sin\widehat{DEN}=\dfrac{1}{2}DE.EN.\dfrac{AM}{\sqrt{AM^2+AE^2}}=...\)
\(\Rightarrow S_{AMND}=S_{AME}-S_{DNE}=...\)


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
là trọng tâm tam giác SAE.
Tứ diện AEND vuông tại đỉnh A nên
Vậy

1.
a.
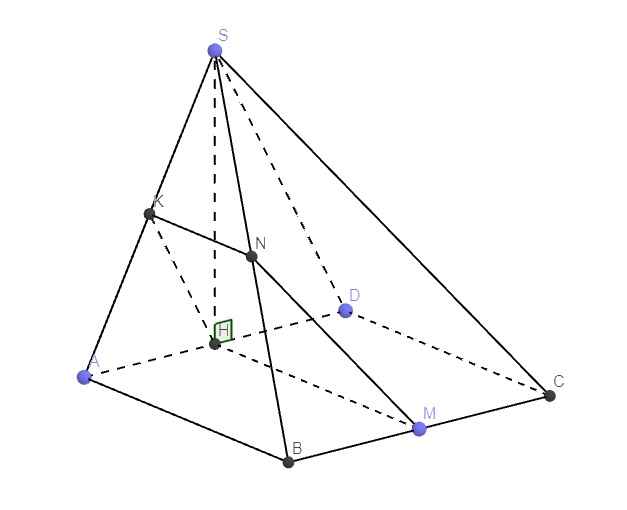
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(\Rightarrow CD\perp SD\Rightarrow\Delta SCD\) vuông tại D
b.
Do H là trung điểm AD, K là trung điểm SA
\(\Rightarrow KH\) là đường trung bình tam giác SAD
\(\Rightarrow KH||SD\Rightarrow KH||\left(SCD\right)\)
H là trung điểm AD, M là trung điểm BC \(\Rightarrow HM||CD\)
\(\Rightarrow HM||\left(SCD\right)\)
Mà HM cắt KH tại H
\(\Rightarrow\left(HKM\right)||\left(SCD\right)\)
c.
Qua K kẻ đường thẳng song song AB cắt SB tại N
\(\Rightarrow N=\left(HKM\right)\cap SB\)
\(\left\{{}\begin{matrix}KN||AB\\HM||AB\end{matrix}\right.\) \(\Rightarrow KN||HM\) (1)
Mặt khác \(\left\{{}\begin{matrix}HM||CD\\CD||\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM\perp KH\) (2)
(1);(2) \(\Rightarrow\) HKNM là hình thang vuông

Đáp án B.
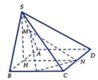
Gọi H là trung điểm của cạnh AB. Khi đó SH ⊥ (ABCD)
Ta có SH ⊥ AB; AB ⊥ HN; HN ⊥ SH và SH = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó: B(1;0;0), A(-1;0;0), N(0;2 3 ;0), C(1;2 3 ;0)
D(-1;2 3 ;0), S(0;0; 3 ), M( - 1 2 ; 0 ; 3 2 ), P(1; 3 ;0)
Mặt phẳng (SCD) nhận
![]()
làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận
![]()
làm một vectơ pháp tuyến.
Gọi φ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
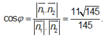
Phân tích phương án nhiễu.
Phương án A: Sai do HS tính đúng
![]()
nhưng lại tính sai ![]() Do đó tính được
Do đó tính được
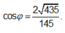
Phương án B: Sai do HS tính đúng ![]() nhưng lại tính sai
nhưng lại tính sai
![]()
Do đó tính được
![]()
Phương án C: Sai do HS tính đúng ![]() nhưng lại tính sai
nhưng lại tính sai
![]() Do đó tính được
Do đó tính được 





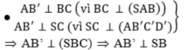
3.
O là trung điểm AC, M là trung điểm SA
\(\Rightarrow\) OM là đường trung bình tam giác SAC
\(\Rightarrow OM//SC\)
Mà \(SC\in\left(SCD\right)\Rightarrow OM//\left(SCD\right)\)
Theo cmt \(OM//SC\Rightarrow OM\in\left(\alpha\right)\)
Qua M kẻ đường thẳng song song AD cắt SD tại P
Qua O kẻ đường thẳng song song AD cắt AB và CD lần lượt tại E và F
\(\Rightarrow\) Hình thang MEFP là thiết diện của \(\left(\alpha\right)\) và chóp
1.
Đề bài ko đúng, tổng của các vecto thì làm sao bằng 1 số được? Bạn có thiếu dấu trị tuyệt đối hay gì đó ko?
2.
\(SA\perp\left(ABCD\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AD\\SA\perp AB\end{matrix}\right.\) \(\Rightarrow\) các tam giác SAD và SAB vuông
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\)
Mà \(BC\perp AB\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\Delta SBC\) vuông tại B
Tương tự \(\left\{{}\begin{matrix}SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\Rightarrow\Delta SCD\) vuông
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(tan\widehat{SBA}=\frac{SA}{AB}=\sqrt{3}\Rightarrow\widehat{SBA}=60^0\)