Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sin a=12/13
cos^2a=1-(12/13)^2=25/169
=>cosa=5/13
tan a=12/13:5/13=12/5
cot a=1:12/5=5/12
sin b=căn 3/2
cos^2b=1-(căn 3/2)^2=1/4
=>cos b=1/2
tan b=căn 3/2:1/2=căn 3
cot b=1/căn 3

Lời giải:
a.
Đồ thị màu xanh lá: $y=\frac{1}{2}x+1$
Đồ thị màu xanh dương: $y=-x-1$
b.
Ta có:
$\tan \alpha=\frac{1}{2}\Rightarrow \alpha=26,57^0$
$\tan \beta = -1\Rightarrow \beta=135^0$

có `cos α=1/2`
`=>cos^2 α=1/4`
Mà `cos^2 α +sin^2 α=1`
`=>1/4+sin^2 α=1`
`=>sin^2 α=1-1/4=3/4`
\(=>sin\alpha=\dfrac{\sqrt{3}}{2}\) (vì `sin α` >0)
ta có `sin α : cos α=tan α`
\(=>tan\alpha=\dfrac{\sqrt{3}}{2}:\dfrac{1}{2}=\sqrt{3}\)
ta có `tan α * cot α =1`
\(=>\sqrt{3}\cdot cot\alpha=1\\ =>cot\alpha=\dfrac{1}{\sqrt{3}}\)
tương tự ta có
\(\left\{{}\begin{matrix}sin\beta=\dfrac{\sqrt{2}}{2}\\cos\beta=1\\cot\beta=1\end{matrix}\right.\)


Vì đã khuya nên não cũng không còn hoạt động tốt nữa, mình làm bài 1 thôi nhé.
Bài 1:
a)
\(2\text{VT}=\sum \frac{2bc}{a^2+2bc}=\sum (1-\frac{a^2}{a^2+2bc})=3-\sum \frac{a^2}{a^2+2bc}\)
Áp dụng BĐT Cauchy-Schwarz:
\(\sum \frac{a^2}{a^2+2bc}\geq \frac{(a+b+c)^2}{a^2+2bc+b^2+2ac+c^2+2ab}=\frac{(a+b+c)^2}{(a+b+c)^2}=1\)
Do đó: \(2\text{VT}\leq 3-1\Rightarrow \text{VT}\leq 1\) (đpcm)
Dấu "=" xảy ra khi $a=b=c$
b)
Áp dụng BĐT Cauchy-Schwarz:
\(\text{VT}=\sum \frac{ab^2}{a^2+2b^2+c^2}=\sum \frac{ab^2}{\frac{a^2+b^2+c^2}{3}+\frac{a^2+b^2+c^2}{3}+\frac{a^2+b^2+c^2}{3}+b^2}\leq \sum \frac{1}{16}\left(\frac{9ab^2}{a^2+b^2+c^2}+\frac{ab^2}{b^2}\right)\)
\(=\frac{1}{16}.\frac{9(ab^2+bc^2+ca^2)}{a^2+b^2+c^2}+\frac{a+b+c}{16}(1)\)
Áp dụng BĐT AM-GM:
\(3(ab^2+bc^2+ca^2)\leq (a^2+b^2+c^2)(a+b+c)\)
\(\Rightarrow \frac{1}{16}.\frac{9(ab^2+bc^2+ca^2)}{a^2+b^2+c^2)}\leq \frac{3}{16}(a+b+c)(2)\)
Từ $(1);(2)\Rightarrow \text{VT}\leq \frac{a+b+c}{4}$ (đpcm)
Dấu "=" xảy ra khi $a=b=c$
Lý giải xíu chỗ $3(ab^2+bc^2+ca^2)\leq (a^2+b^2+c^2)(a+b+c)$ cho bạn nào chưa rõ:
Áp dụng BĐT AM-GM:
$(a^2+b^2+c^2)(a+b+c)=(a^3+ac^2)+(b^3+a^2b)+(c^3+b^2c)+(ab^2+bc^2+ca^2)$
$\geq 2a^2c+2ab^2+2bc^2+(ab^2+bc^2+ca^2)=3(ab^2+bc^2+ca^2)$

a) - Với hàm số y = x + 1
Cho x = 0 y = 1 được A(0; 1)
Cho y = 0 x = -1 được B(-1; 0)
Nối A, B được đường thẳng y = x + 1
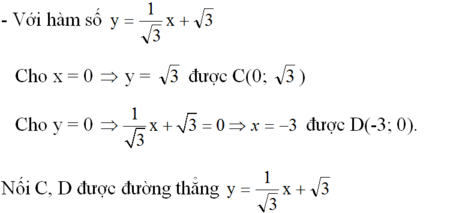
- Với hàm số y = √3 x - √3
Cho x = 0 => y = -√3 được E(0; -√3)
Cho y = 0 => x = 1 được F(1; 0).
Nối E, F được đường thẳng y = √3 x - √3
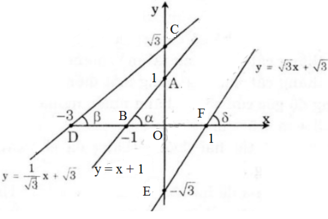
b) Ta có:
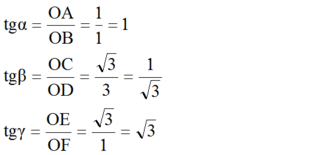
Suy ra α = 45o, β = 30o, γ = 60o
a) Đồ thị như hình bên.
b) tgα = = 1,
= 1,
tgβ =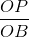 =
= 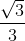 =
= 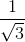 ,
,
tgɣ =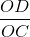 =
= 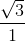 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .
a) Đồ thị như hình bên.
b) tgα =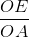 = 1,
= 1,
tgβ =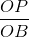 =
= 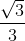 =
= 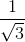 ,
,
tgɣ =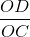 =
= 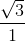 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .