Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nhận xét: Các số hữu tỉ âm luôn nhỏ hơn các số hữu tỉ dương. Do đó ta chỉ cần so sánh các số hữu tỉ âm với nhau và các số hữu tỉ dương với nhau.
+ So sánh các số hữu tỉ âm trong dãy: 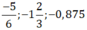
Ta có:
![]()
Vì 24 > 0, -40 < -21 < -20 nên 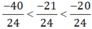 hay
hay 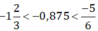
+ So sánh các số hữu tỉ dương trong dãy: 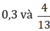 .
.
Ta có:
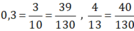
Vì 39 < 40 nên 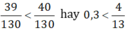 .
.
Vậy ta được dãy sắp theo thứ tự lớn dần như sau:
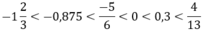


Viết các phân số dưới dạng tối giản:
- So sánh các số hữu tỉ dương với nhau:
Ta có :
Vì 39 < 40 và 130 > 0 nên
- Tương tự So sánh các số hữu tỉ âm với nhau
Vậy:
Các số hữu tỉ được sắp sếp theo thứ tự lớn dần là:
\(-0,875< -\frac{5}{6}< -\frac{1}{3}< 0< 0,3\)
![]() ^...^
^...^ ![]() ^_^
^_^

a) Ta có:
\(6 = \sqrt {36} ; - 1,7 = - \sqrt {2,89} \)
Vì 0 < 2,89 < 3 nên 0> \( - \sqrt {2,89} > - \sqrt 3 \) hay 0 > -1,7 > \( - \sqrt 3 \)
Vì 0 < 35 < 36 < 47 nên \(0 < \sqrt {35} < \sqrt {36} < \sqrt {47} \) hay 0 < \(\sqrt {35} < 6 < \sqrt {47} \)
Vậy các số theo thứ tự tăng dần là: \( - \sqrt 3 ; - 1,7;0;\sqrt {35} ;6;\sqrt {47} \)
b) Ta có:
\(\sqrt {5\frac{1}{6}} = \sqrt {5,1(6)} ; - \sqrt {2\frac{1}{3}} = - \sqrt {2,(3)} \); -1,5 = \( - \sqrt {2,25} \)
Vì 0 < 2,25 < 2,3 < 2,(3) nên 0> \( - \sqrt {2,25} > - \sqrt {2,3} > - \sqrt {2,(3)} \) hay 0 > -1,5 > \( - \sqrt {2,3} > - \sqrt {2\frac{1}{3}} \)
Vì 5,3 > 5,1(6) > 0 nên \(\sqrt {5,3} > \sqrt {5,1(6)} \)> 0 hay \(\sqrt {5,3} > \sqrt {5\frac{1}{6}} > 0\)
Vậy các số theo thứ tự giảm dần là: \(\sqrt {5,3} ;\sqrt {5\frac{1}{6}} ;0\); -1,5; \( - \sqrt {2,3} ; - \sqrt {2\frac{1}{3}} \)

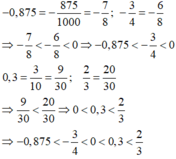
\(a;0,\left(35\right)=0,3\left(53\right)>0,353\)
\(b;2,1\left(14\right)< 2,15< 2,\left(15\right)< 2,1\left(5\right)\)