Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

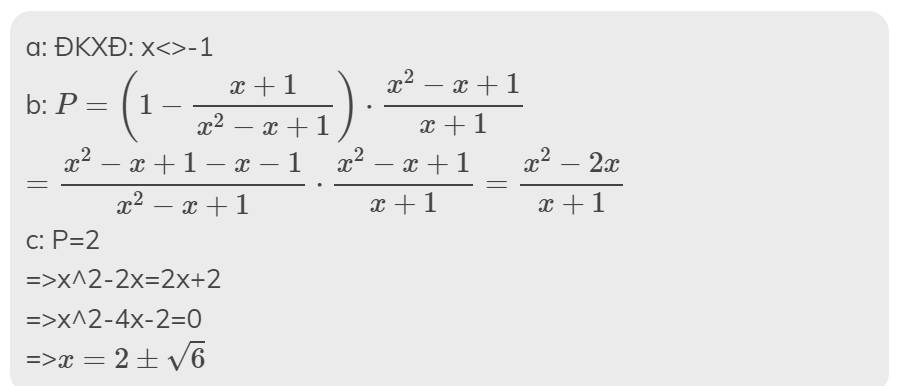
a: ĐKXĐ: x<>-1
b: \(P=\left(1-\dfrac{x+1}{x^2-x+1}\right)\cdot\dfrac{x^2-x+1}{x+1}\)
\(=\dfrac{x^2-x+1-x-1}{x^2-x+1}\cdot\dfrac{x^2-x+1}{x+1}=\dfrac{x^2-2x}{x+1}\)
c: P=2
=>x^2-2x=2x+2
=>x^2-4x-2=0
=>\(x=2\pm\sqrt{6}\)

a)Để biểu thức vô nghĩa thì \(\left[{}\begin{matrix}x+2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\Leftrightarrow x\in\left\{-2;1\right\}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x+2\ne0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-2\\x\ne1\end{matrix}\right.\Leftrightarrow x\notin\left\{-2;1\right\}\)
b) Ta có: \(\dfrac{5x-2}{12}-\dfrac{2x^2+1}{8}=\dfrac{x-3}{6}+\dfrac{1-x^2}{4}\)
\(\Leftrightarrow\dfrac{2\left(5x-2\right)}{24}-\dfrac{3\left(2x^2+1\right)}{24}=\dfrac{4\left(x-3\right)}{24}+\dfrac{6\left(1-x^2\right)}{24}\)
\(\Leftrightarrow10x-4-6x^2-3=4x-12+6-6x^2\)
\(\Leftrightarrow-6x^2+10x-7+6x^2-4x+6=0\)
\(\Leftrightarrow6x-1=0\)
\(\Leftrightarrow6x=1\)
\(\Leftrightarrow x=\dfrac{1}{6}\)
Vậy: \(S=\left\{\dfrac{1}{6}\right\}\)

Đặt bthuc = A nhé
ĐKXĐ : \(2x\ne3y\)
\(A=\left[\dfrac{2x\left(4x^2+6xy+9y^2\right)}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}-\dfrac{27y^3+36xy^2}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}-\dfrac{24xy\left(2x-3y\right)}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}\right]\left[\dfrac{2x\left(2x-3y\right)}{\left(2x-3y\right)}+\dfrac{9y^2+12xy}{\left(2x-3y\right)}\right]\)\(=\left[\dfrac{8x^3+12x^2y+18xy^2-27y^3-36xy^2-48x^2y+72xy^2}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}\right]\left[\dfrac{4x^2-6xy+9y^2+12xy}{\left(2x-3y\right)}\right]\)
\(=\dfrac{8x^3-36x^2y+36xy^2-27y^3}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}\cdot\dfrac{4x^2+6xy+9y^2}{2x-3y}\)
\(=\dfrac{\left(2x-3y\right)^3}{\left(2x-3y\right)^2}=2x-3y\)
Với x = 1/3 ; y = -2 (tmđk) thay vào A ta được : A = 2.1/3 - 3.(-2) = 20/3

\(a,ĐK:x\ne\pm2\\ b,A=\dfrac{x^2+4x+4+x^2-4x+4+16}{2\left(x-2\right)\left(x+2\right)}\\ A=\dfrac{2x^2+32}{2\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+16}{x^2-4}\\ c,A=-3\Leftrightarrow-3x^2+12=x^2+16\\ \Leftrightarrow4x^2=-4\Leftrightarrow x\in\varnothing\)



1)
a) Biểu thức \(\dfrac{x-2}{x^2+8x}\) vô nghĩa khi \(x^2+8x=0\)
\(\Leftrightarrow x\left(x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
Vậy: Khi \(x\in\left\{0;-8\right\}\) thì biểu thức \(\dfrac{x-2}{x^2+8x}\) vô nghĩa
b) Biểu thức \(\dfrac{25x^2-1}{16x^2-25}\) vô nghĩa khi \(16x^2-25=0\)
\(\Leftrightarrow\left(4x-5\right)\left(4x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-5=0\\4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=5\\4x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
Vậy: Khi \(x\in\left\{\dfrac{5}{4};-\dfrac{5}{4}\right\}\) thì biểu thức \(\dfrac{25x^2-1}{16x^2-25}\) vô nghĩa
c) Biểu thức \(\dfrac{x^2+1}{2x^2-28x+98}\) vô nghĩa khi \(2x^2-28x+98=0\)
\(\Leftrightarrow2\left(x^2-14x+49\right)=0\)
\(\Leftrightarrow\left(x-7\right)^2=0\)
\(\Leftrightarrow x-7=0\)
hay x=7
Vậy: Khi x=7 thì biểu thức \(\dfrac{x^2+1}{2x^2-28x+98}\) vô nghĩa
d) Để biểu thức \(\dfrac{2x+3}{9-\left(x+3\right)^2}\) vô nghĩa thì \(9-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(3-x-3\right)\left(3+x+3\right)=0\)
\(\Leftrightarrow-x\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)
Vậy: Khi \(x\in\left\{0;-6\right\}\) thì biểu thức \(\dfrac{2x+3}{9-\left(x+3\right)^2}\) vô nghĩa
2)
a) ĐKXĐ: \(x\notin\left\{0;-8\right\}\)
b) ĐKXĐ: \(x\notin\left\{\dfrac{5}{4};-\dfrac{5}{4}\right\}\)
c) ĐKXĐ: \(x\ne7\)
d) ĐKXĐ: \(x\notin\left\{0;-6\right\}\)
3)
a) Để phân thức \(\dfrac{x-2}{x^2+8x}=0\) thì x-2=0
hay x=2(nhận)
Vậy: Khi x=2 thì phân thức \(\dfrac{x-2}{x^2+8x}=0\)
b) Để phân thức \(\dfrac{25x^2-1}{16x^2-25}=0\) thì \(25x^2-1=0\)
\(\Leftrightarrow\left(5x-1\right)\left(5x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=0\\5x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=1\\5x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\left(nhận\right)\\x=-\dfrac{1}{5}\left(nhận\right)\end{matrix}\right.\)
Vậy: Khi \(x\in\left\{\dfrac{1}{5};-\dfrac{1}{5}\right\}\) thì phân thức \(\dfrac{25x^2-1}{16x^2-25}=0\)
c) Để phân thức \(\dfrac{x^2+1}{2x^2-28x+98}=0\) thì \(x^2+1=0\)
mà \(x^2+1>0\forall x\) thỏa mãn ĐKXĐ
nên \(x\in\varnothing\)
Vậy: Không có giá trị nào của x để \(\dfrac{x^2+1}{2x^2-28x+98}=0\)
d) Để phân thức \(\dfrac{2x+3}{9-\left(x+3\right)^2}=0\) thì 2x+3=0
\(\Leftrightarrow2x=-3\)
hay \(x=-\dfrac{3}{2}\)(nhận)
Vậy: Khi \(x=-\dfrac{3}{2}\) thì phân thức \(\dfrac{2x+3}{9-\left(x+3\right)^2}=0\)
mình chỉ làm 1 câu thôi nhé các câu khác làm tương tự
1. biểu thức vô nghĩa <=> mẫu thức = 0
\(x^2+8x=0< =>\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
vậy ...
2. tập xác định là tập hợp các giá trị làm phân thức có nghĩa (trong căn thì ≥ 0 ; dưới mẫu thì ≠ 0)
\(x^2+8x\ne0< =>\left[{}\begin{matrix}x\ne0\\x\ne-8\end{matrix}\right.\)
vậy ...
3. để phân thức = 0 => tử bằng không và mẫu khác không
\(\left\{{}\begin{matrix}x-2=0\\x^2+8x\ne0\end{matrix}\right.< =>\left\{{}\begin{matrix}x=2\left(tm\right)\\\left[{}\begin{matrix}x\ne0\\x\ne-8\end{matrix}\right.\end{matrix}\right.\)