Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b, Ta có \(P=\frac{x\sqrt{x}-\sqrt{x}}{x}=\frac{x-1}{\sqrt{x}}>0\)
\(\Rightarrow\hept{\begin{cases}x-1\ne0\\x-1>0\\x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne1\\x>1\\x\ne0\end{cases}}\)

a)
\(1+tan^2a=\frac{1}{cos^2a}\)
\(1+3^2=\frac{1}{cos^2a}\)
\(10=\frac{1}{cos^2a}\)
\(cos^2a=\frac{1}{10}\)
\(cosa=\pm\sqrt{\frac{1}{10}}=\pm\frac{1}{\sqrt{10}}\)
\(sin^2a+cos^2a=1\)
\(sin^2a+\frac{1}{10}=1\)
\(sin^2a=\frac{9}{10}\)
\(sina=\pm\sqrt{\frac{9}{10}}=\pm\frac{3}{\sqrt{10}}\)
Vì tan = 3 nên M có 2 trường hợp :
TH1 :
sin và cos cùng dương
\(\Rightarrow M=\frac{\frac{1}{\sqrt{10}}+\frac{3}{\sqrt{10}}}{\frac{1}{\sqrt{10}}-\frac{3}{\sqrt{10}}}\)
\(=\frac{\frac{4}{\sqrt{10}}}{-\frac{2}{\sqrt{10}}}\)
= -2
TH2 :
Cả sin và cos cùng âm
\(\Rightarrow M=\frac{-\frac{1}{\sqrt{10}}+\left(-\frac{3}{\sqrt{10}}\right)}{-\frac{1}{\sqrt{10}}-\left(-\frac{3}{\sqrt{10}}\right)}\)
=\(\frac{-\frac{4}{\sqrt{10}}}{\frac{2}{\sqrt{10}}}\)
= -2
b)
\(B=\frac{sin15+cos15}{cos15}-cot75\)
=\(\frac{sin15}{cos15}+\frac{cos15}{cos15}-cot75\)
=\(tan15+1-cot75\)
=\(cot75+1-cot75\)
= 1

a) AM ứng với cạnh huyền BC nên AM = \(\frac{1}{2}\) x BC = \(\frac{4}{2}\) = 2 cm
AH = tan\(\widehat{ACH}\)x HM = tan 150 x 2 = \(4-2\sqrt{3}\)cm
Sin \(\widehat{AMH}\)= \(\frac{AH}{AM}\)= \(\frac{4-2\sqrt{3}}{2}\) = \(2-\sqrt{3}\) cm
Định lí Pitago : AM2 = AH2 + HM2
HC = tan \(\widehat{ACH}\)x AH

Bài 1 :
a) \(Cos30^o=Cos\left(2.15^o\right)=2cos^215^o-1\)
\(\Rightarrow cos^215^o=\dfrac{cos30^o+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\dfrac{\sqrt[]{3}}{2}+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\sqrt[]{3}+2}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\sqrt[]{3}+2}}{2}\)
\(\Rightarrow cos15^o=\dfrac{2\sqrt[]{\sqrt[]{3}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{4\sqrt[]{3}+8}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6+2.2\sqrt[]{2}\sqrt[]{6}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\left(\sqrt[]{6}+\sqrt[]{2}\right)^2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6}+\sqrt[]{2}^{ }}{4}\left(dpcm\right)\)
a)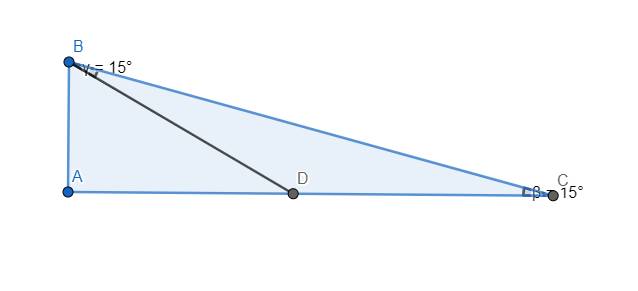
Dựng tam giác ABC vuông tại A với \(\widehat{C}=15^o\). Trên đoạn thẳng AC lấy điểm D sao cho \(\widehat{CBD}=15^o\). Không mất tính tổng quát, ta chuẩn hóa \(AB=1\). \(\Rightarrow\left\{{}\begin{matrix}BD=\dfrac{AB}{cos60^o}=2\\AD=AB.tan60^o=\sqrt{3}\end{matrix}\right.\)
Dễ thấy tam giác DBC cân tại D \(\Rightarrow BD=CD=2\) \(\Rightarrow AC=AD+DC=2+\sqrt{3}\)
\(\Rightarrow tanC=\dfrac{AB}{AC}=\dfrac{1}{2+\sqrt{3}}=2-\sqrt{3}\)
\(\Rightarrow\dfrac{sinC}{cosC}=2-\sqrt{3}\)
\(\Rightarrow sinC=\left(2-\sqrt{3}\right)cosC\)
Mà \(sin^2C+cos^2C=1\)
\(\Rightarrow\left(7-4\sqrt{3}\right)cos^2C+cos^2C=1\)
\(\Leftrightarrow\left(8-4\sqrt{3}\right)cos^2C=1\)
\(\Leftrightarrow cos^2C=\dfrac{1}{8-4\sqrt{3}}=\dfrac{2+\sqrt{3}}{4}\)
\(\Leftrightarrow cosC=\sqrt{\dfrac{2+\sqrt{3}}{4}}\) \(=\dfrac{\sqrt{2+\sqrt{3}}}{2}=\dfrac{\sqrt{8+4\sqrt{3}}}{4}\) \(=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
a) Đầu tiên bạn tự đi chứng minh hai công thức sau, do quá dài nên bạn có thể lên mạng tham khảo cách chứng minh:
\(\sin2a=2\sin a.\cos a\)
\(cos2a=cos^2a-sin^2a\)
Áp dụng hai công thức trên ta có:
\(sin30^o=2sin15^ocos15^o\Leftrightarrow sin15^ocos15^o=\frac{1}{4}\Leftrightarrow cos15^o=\frac{1}{4sin15^o}\)
\(cos30^o=cos^215^o-sin^215^o\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}=cos^215^o-sin^215^o\)
\(\Leftrightarrow\left(\frac{1}{4sin^215^o}\right)^2-sin^215^o=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow\frac{1}{16sin^415^o}-sin^215^o=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow-32sin^415^o-16sin^215^o\sqrt{3}+2=0\)
\(\Leftrightarrow sin^215^o=\frac{2-\sqrt{3}}{4}\left(sin^215^o\ge0\right)\)
\(\Leftrightarrow sin15^o=\sqrt{\frac{2-\sqrt{3}}{4}}=\sqrt{\frac{\left(\sqrt{3}-1\right)^2}{4\sqrt{2}}}=\frac{\sqrt{3}-1}{2\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}\left(đpcm\right)\)