Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
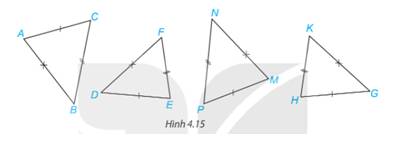
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)

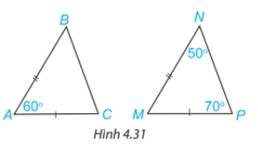
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Vì góc A trong tam giác ABC là góc tù
=> Cạnh đối diện nó là cạnh lớn nhất
=> Cạnh BC lớn nhất
B C A

b nha
bạn dương thảo là trai hay gái vậy ?
là gái mình kb nha

bạn viết đề lại đi
hình như thiếu
... Từ C kẻ tia Cx cắt BA tại E (sao cho)...

Bài 40:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
Ta có: BA=BE
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
c: Ta có: AD=DE
mà DE<DC
nên AD<DC
d: Ta có: ΔADF=ΔEDC
nên AF=EC
Xét ΔBFC có
\(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
Do đó: AE//CF
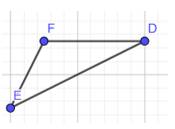

a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
\( \Rightarrow \) F > 90° do F là góc tù
\( \Rightarrow \) D + E < 180° - 90°
\( \Rightarrow \) F là góc lớn nhất trong tam giác DEF
\( \Rightarrow \) Cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF
\( \Rightarrow \) DE là cạnh lớn nhất
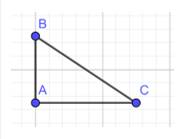
b) Tam giác ABC có góc A là góc vuông nên ta có
\( \Rightarrow \widehat B + \widehat C = {90^o} \Rightarrow \widehat B;\widehat C < {90^o}\)
\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \)BC là cạnh lớn nhất tam giác ABC do đối diện góc A