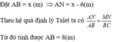Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

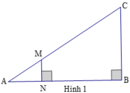
a, ∠ANM = ∠CBN (=90 độ) (chúng ở vị trí đồng vị)
=> MN//BC , theo hệ quả định lý Talet ta có:
AN/AB = MN/BC, cho AB=x (cm) thì AN = x-6 (cm)
Nên: (x-6)/x=1,5/6 => x=8(cm)
Nên AB = 8 cm
b, AD là đường phân giác của tam giác ABC nên:
AB/AC = BD/DC, nếu cho BD=x (cm) thì ta có DC=5-x (cm)
Nên: 4/6=x/(5-x) => 20=10x => x=2 (cm), nên BD= 2 cm
=> DC=3 cm
Theo hình vẽ ta có: AC//BE => ∠ACD = ∠DBE (so le trong)
Xét △BDE và △CDA có:
∠ACD=∠DBE (c/m tr)
∠ADC=∠BDE (đối đỉnh)
=> △BDE=△CDA (g.g)
=> BE/AC = BD/CD => BE/6=2/3 => BE=12:3=4 (cm)
Vậy: BD= 2 cm
BE= 4 cm

Theo tính chất tia phân giác và tính chất dãy tỉ số bằng nhau ta có:
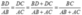
Từ BE//AC nên chứng minh được DABE cân tại B Þ BE = 4cm

a,Xét ∆ABC và ∆KBA có :
B là góc chung
BAC = BKA
=> ∆ ABC ĐỒNG DẠNG với ∆KBA
=>BA TRên KB = BC TRÊN BA
=>AB²= BK.BC
https://h.vn/hoi-dap/question/585511.html
Bạn xem cả bài ở link này đi(mik gửi cho)
Học tôt!!!!!!!!!!!!