Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(MA \bot \left( P \right)\) (A là hình chiếu của M trên (P))
\(NB \bot \left( P \right)\) (B là hình chiếu của N trên (P))
\( \Rightarrow \) MA // NB \( \Rightarrow \) 4 điểm M, A, B, N đồng phẳng
\(\left. \begin{array}{l}\left( {AMNB} \right) \cap \left( P \right) = AB\\a//\left( P \right)\end{array} \right\} \Rightarrow a//AB\)
\( \Rightarrow \) Tứ giác AMNB là hình bình hành.
Mà \(MA \bot AB\left( {MA \bot \left( P \right)} \right)\)
\( \Rightarrow \) Tứ giác AMNB là hình chữ nhật nên MA = NB
Vậy M, N có cùng khoảng cách đến (P).

tham khảo:
a) Vì M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) nên hình chiếu của a trên mặt phẳng (P) là a’ đường thẳng đi qua hai điểm M', N'.
b) b vuông góc với M'N' và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); M'N' cắt MM' tại M' do đó b vuông góc mặt phẳng tạo bởi M'N', MM' suy ra b có vuông góc với a.
c) b vuông góc với a và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); a cắt MM' tại M do đó b vuông góc mặt phẳng tạo bởi a, MM' suy ra b có vuông góc với M'N'.

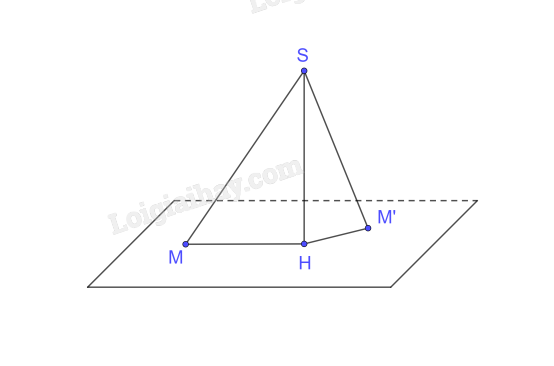
a)
+) Giả sử SM = SM’
Xét tam giác SHM vuông tại H có
\(S{M^2} = S{H^2} + M{H^2}\) (định lí Pytago)
Xét tam giác SHM’ vuông tại H có
\(S{M'^2} = S{H^2} + M'{H^2}\) (định lí Pytago)
Mà SM = SM’ nên MH = MH’
+) Giả sử HM = HM’
Xét tam giác SHM vuông tại H có
\(S{M^2} = S{H^2} + M{H^2}\) (định lí Pytago)
Xét tam giác SHM’ vuông tại H có
\(S{M'^2} = S{H^2} + M'{H^2}\) (định lí Pytago)
Mà HM = HM’ nên SM = SM’
b) \(\begin{array}{l}MH > M'H \Leftrightarrow M{H^2} > M'{H^2}\\ \Leftrightarrow M{H^2} + S{H^2} > M'{H^2} + S{H^2} \Leftrightarrow S{M^2} > S{{M'}^2} \Leftrightarrow SM > SM'\end{array}\)

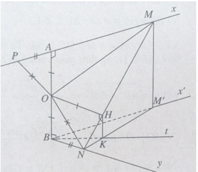
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
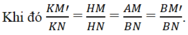
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

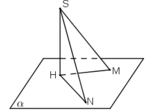
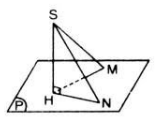
Giả sử ta có hai đường xiên SM, SN và các hình chiếu HM, HN của chúng trên mp (α).
Vì SH ⊥ mp(α)
⇒ SH ⊥ HM và SH ⊥ HN
⇒ ΔSHN và ΔSHM vuông tại H.
Áp dụng định lí Py-ta- go vào hai tam giác vuông này ta có:
⇒ S M 2 = S H 2 + H M 2 ; v à S N 2 = S H 2 + H N 2 . a ) S M = S N ⇔ S M 2 = S N 2 ⇔ H M 2 = H N 2 ⇔ H M = H N . b ) S M > S N ⇔ S M 2 > S N 2 ⇔ H M 2 > H N 2 ⇔ H M > H N .

a) Ta có:
\(\left. \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( P \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).
b) Ta có:
\(\left. \begin{array}{l}AH \bot \left( Q \right)\\BK \bot \left( Q \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( Q \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).

a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB của chúng trên mp(α)
Giả sử HA = HB
Vì SH ⊥ mp(α) nên SH ⊥ HA và SH ⊥ SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có canh SH chung và HA = HB nên :
ΔSHA = ΔSHB SA = SB
Ngược lại nếu SA = SB thì ΔSHA = ΔSHB ⇒ HA = HB
Kết quả, ta có HA = HB SA= SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(α) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B' sao cho HA' = HA ⇒ HC > HA'. Như vậy, theo kết quả câu a) ta có SA' = SA. Ta có trong các tam giác vuông SHB', SHC thì :
SC2= SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA' nên SC2 > SA2 ⇒ SC > SA
Suy ra SC > SA
Như vậy HC > HA ⇒ SC > SA
Lí luận tương tự, ta có : SC > SA ⇒ HC > HA
Kết quả : HC > HA ⇔ SC > SA
a) Gọi SN là một đường xiên khác. Xét hai tam giác vuông SHM và SHN có SH chung. Nếu SM = SN => tam giác SHM = tam giác SHN => HM = HN, ngược lại nếu HM = HN thì tam giác SHM = tam giác SHNSM => SM = SN.
b) Xét tam giác vuông SHM và SHN có SH chung. Nếu SN > SM thì \(HN^2-SN^2-SH^2\) => \(SM^2-SH^2=HM^2\) => HN > HM. Chứng minh tương tự cho chiều ngược lại.
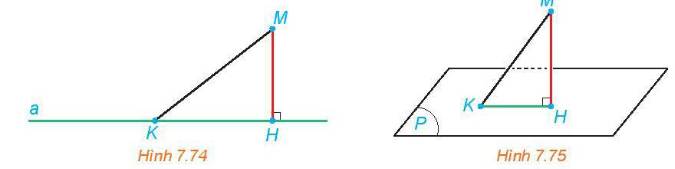






a) Vì H là hình chiếu của M trên đường thẳng a, nên MH là khoảng cách từ M đến a và MH là đoạn thẳng ngắn nhất từ M đến a, suy ra MK ≥ MH.
b) Vì H là hình chiếu của M trên (P) nên MH vuông góc với (P) do đó MH vuông góc với HK.
Dựa vào mối quan hệ đường xiên và đường vuông góc ta có MK ≥ MH.