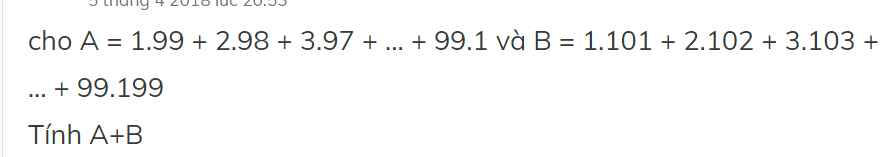Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A+B = (1.99+2.98+3.97+...+99.1)+(1.101+2.102+3.103+...+99.199)
A+B = (1.99+1.101)+(2.98+2.102)+(3.97+3.103)+...+(99.1+99.199)
A+B = 1(99+101) + 2(98+102) + 3(97.103)+...+99(1+199)
A+B = 1.200 + 2.200 + 3.200 +...+ 99.200
A+B = 200.(1+2+3+...+200)
A+B = 200.4950
A+B = 990000

A + B = ( 1 . 99 + 2 . 98 + 3 . 97 + ... + 99 . 1 ) + ( 1 . 101 + 2 . 102 + 3 . 103 + ... + 99 . 199 )
A + B = 99 . ( 1 + 199 ) + 98 . ( 2 + 198 ) + 97 . ( 3 + 197 ) + ... + 2 . ( 102 + 98 ) + 1 . ( 99 + 101 )
A + B = 99 . 200 + 98 . 200 + 97 . 200 + ... + 2 . 200 + 1 . 200
A + B = ( 99 + 98 + 97 + ... + 2 + 1 ) . 200
A + B = 4950 . 200
A + B = 990000

A+B=(1.99+2.98+...+99.1)+(1.101+2.102+...+99.199)
=(1.99+1.101)+(2.98+2.102)+...+(99.1+99.199)
=1.(99+101)+2.(98+102)+...+99(1+199)
=200+2.200+...+99.200
=200.(1+2+3+4+...+99)
=200.4950
=.....



Lâu rồi mk ko làm nên ko bt đúng ko, ý B để mk xem xét đã nha


th1 n=2\(A=\frac{12.2+1}{30.2+1}=\frac{25}{61}\)
th2 n=5 \(A=\frac{12.5+1}{30.5+1}=\frac{61}{151}\)
Gọi ƯCLN(12n+1,30n+1) là d đk d thuộc N*
ta có vì 12n+1 chia hết cho d suy ra 60n+5 chia hết cho d
30n+1 chia hết cho d suy ra 60n+2 chia hết cho d
suy ra 60n+5-(60n+2) chia hết cho d
3 chia hết cho d
d thuộc ước của 3
Ư(3)={1;3}
ta có vì 60n+5 ko thể chia hết cho 3
60n+2 ko chia hết cho 3
suy ra d=1
Vì ƯCLN(12n+1,30n+1)=1 suy ra đây là hai số nguyên tố cùng nhau và A là tối giản