Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

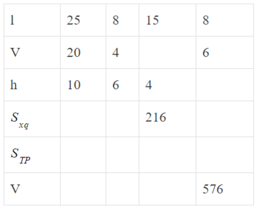
| l | 25 | 8 | 15 | 8 |
| V | 20 | 4 | 12 | 6 |
| h | 10 | 6 | 4 | 12 |
| S x q | 900 | 144 | 216 | 336 |
| S T P | 1900 | 208 | 576 | 432 |
| V | 500 | 192 | 720 | 576 |

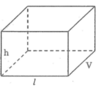
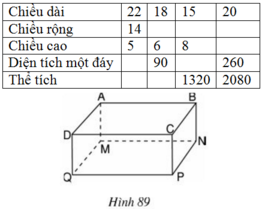
a) Thể tích hình hộp chữ nhật ABCD.MNPQ là:
V = NM.NP.NB
b) Ta có công thức:
Thể tích = chiều dài x chiều rộng x chiều cao.
Diện tích một đáy = chiều dài x chiều rộng.
+ Cột 1: Chiều dài = 22; Chiều rộng = 14; chiều cao = 5.
Thể tích = 22.14.5 = 1540
Diện tích một đáy = 22.14 = 308.
+ Cột 2: Chiều dài = 18; chiều cao = 6; diện tích một đáy = 90
chiều rộng = 90 : 18 = 5
thể tích = 18.5.6 = 540.
+ Cột 3: chiều dài = 15; chiều cao = 8; thể tích = 1320
chiều rộng = 1320 : 15 : 8 = 11
Diện tích một đáy = 11.15 = 165
+ Cột 4 : chiều dài = 20; diện tích một đáy = 260; thể tích = 2080
chiều rộng = 260 : 20 = 13
chiều cao = 2080 : 260 = 8.
Vậy ta có bảng hoàn chỉnh dưới đây:
| Chiều dài | 22 | 18 | 15 | 20 |
| Chiều rộng | 14 | 5 | 11 | 13 |
| Chiều cao | 5 | 6 | 8 | 8 |
| Diện tích một đáy | 308 | 90 | 165 | 260 |
| Thể tích | 1540 | 540 | 1320 | 2080 |

| l | 25 | 8 | 15 | 8 |
| v | 20 | 4 | 12 | 6 |
| h | 10 | 6 | 4 | 12 |
| Sxq | 900 | 144 | 216 | 336 |
| Stp | 1900 | 208 | 576 | 432 |
| V | 5000 | 192 | 720 | 576 |

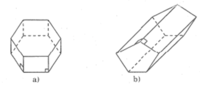
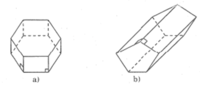
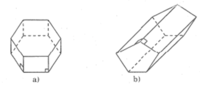
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Công thức liên hệ giữa m,n,d,c :
m = n + 2 ; d = 2n; c = 3n

| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Không thể làm một hình lăng trụ đứng có 15 đỉnh vì d = 2n (số đỉnh của hình lăng trụ là một số chẵn)

| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Số cạnh của một đáy là: n = d/2 = 20/2 = 10 cạnh
Hình lăng trụ có 20 đỉnh thì :
Số mặt là m = n + 2 = 10 + 2 = 12 mặt
Số cạnh là c = 3n = 3.10 = 30 cạnh
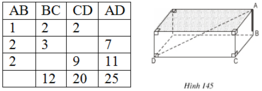
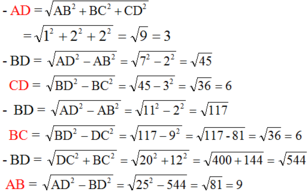


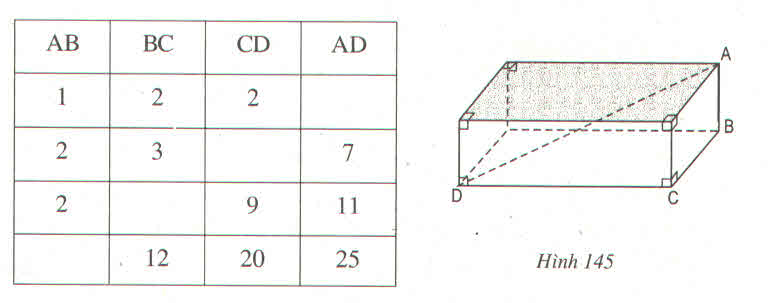
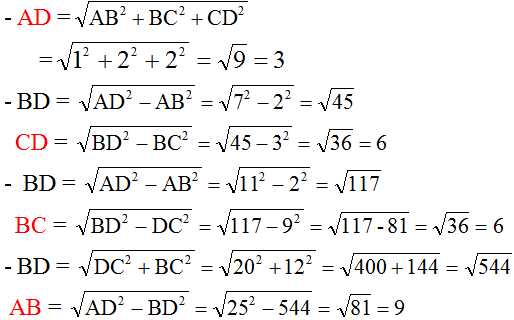 Ta có bảng sau:
Ta có bảng sau: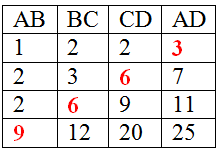


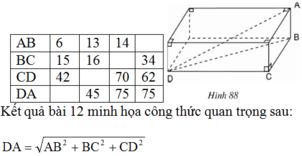
Trước hết ta chứng minh hệ thức: DA2 = AB2 + BC2 + CD2.
+ ΔBCD vuông tại C suy ra: BD2 = BC2 + CD2 .
+ ΔABD vuông tại B ⇒ AD2 = AB2 + BD2
Mà BD2 = BC2 + CD2 ⇒ AD2 = AB2 + BC2 + CD2 .
Vậy AD2 = AB2 + BC2 + CD2 .
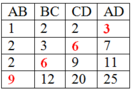
Áp dụng hệ thức trên để tính các cạnh còn thiếu trong bảng ta có:
+ Cột 1: AB = 6; BC = 15; CD = 42
⇒AD2 = AB2 + BC2 + CD2 = 62 + 152 + 422 = 2025
⇒AD = 45.
+ Cột 2: AB = 13; BC = 16; AD = 45
⇒CD2 = AD2 - AB2 - BC2 = 452 - 132 - 162 = 1600
⇒CD = 40.
+ Cột 3: AB = 14; CD = 70; DA = 75
⇒BC2 = DA2 - CD2 - AB2 = 752 - 702 - 142 = 529
⇒BC = 23
+ Cột 4: BC = 34; CD = 62; DA = 75
⇒AB2 = DA2 - BC2 - CD2 = 752 - 342 - 622 = 625
⇒AB = 25.
Vậy ta có kết quả như bảng sau: