Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B6:
Ta có: \(\hept{\begin{cases}P\left(-1\right)=a-b+c\\P\left(-2\right)=4a-2b+c\end{cases}}\)
=> \(P\left(-1\right)+P\left(-2\right)=5a-3b+2c\)
Mà theo đề bài \(5a-3b+2c=0\)
=> \(P\left(-1\right)+P\left(-2\right)=0\Rightarrow P\left(-1\right)=-P\left(-2\right)\)
Thay vào ta được: \(P\left(-1\right).P\left(-2\right)=-P\left(-2\right).P\left(-2\right)=-P\left(-2\right)^2\le0\left(\forall a,b,c\right)\)
=> đpcm
B5:
Ta có:
P+Q+R
= 5x2y2-xy-2y3-y2+5x4-2x2y2-5xy+y3-3y2+2x4-x2y2+6xy+y3+6y2+7
= x2y2+2y2+7x4+7
Mà \(x^2y^2\ge0;2y^2\ge0;7x^4\ge0\left(\forall x,y\right)\)
=> \(x^2y^2+2y^2+7x^4+7\ge7\)
=> Tổng 3 đa thức P,Q,R luôn dương
=> Trong 3 đa thức đó luôn tồn tại 1 đa thức lớn hơn 0
=> đpcm

Lời giải:
$x+y-2=0\Rightarrow x+y=2$
a)
$B=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x(x+y)+2x+3$
$=x^3(x+y)+x^3y-2x^3+x^2y^2-2x^2y-2x+2x+3$
$=2x^3+x^3y-2x^3+x^2y^2-2x^2y+3$
$=x^3y+x^2y^2-2x^2y+3$
$=xy(x^2+xy-2x)+3=xy[x(x+y)-2x]+3=xy(2x-2x)+3=3$
b)
$C=x^3+x^2y-2x^2-xy+y^2-3y-x+5$
$=x^2(x+y)-2x^2-xy+y^2-3(y+x)+2x+5$
$=2x^2-2x^2-xy+y^2-6+2x+5$
$=-xy+y^2+2x-1$
$=y(x+y)+2x-1-2xy=2y+2x-1-2x=2(x+y)-1-2x=3-2x$ (không tính cụ thể được giá trị- bạn xem lại đề)
c)
$D=2x^4+3x^2y^2+y^4+y^2$
$=(x^4+2x^2y^2+y^4)+x^4+x^2y^2+y^2
$=(x^2+y^2)^2+x^4+x^2y^2+y^2$
$=1+x^2(x^2+y^2)+y^2=1+x^2+y^2=1+1=2$

`@` `\text {Ans}`
`\downarrow`

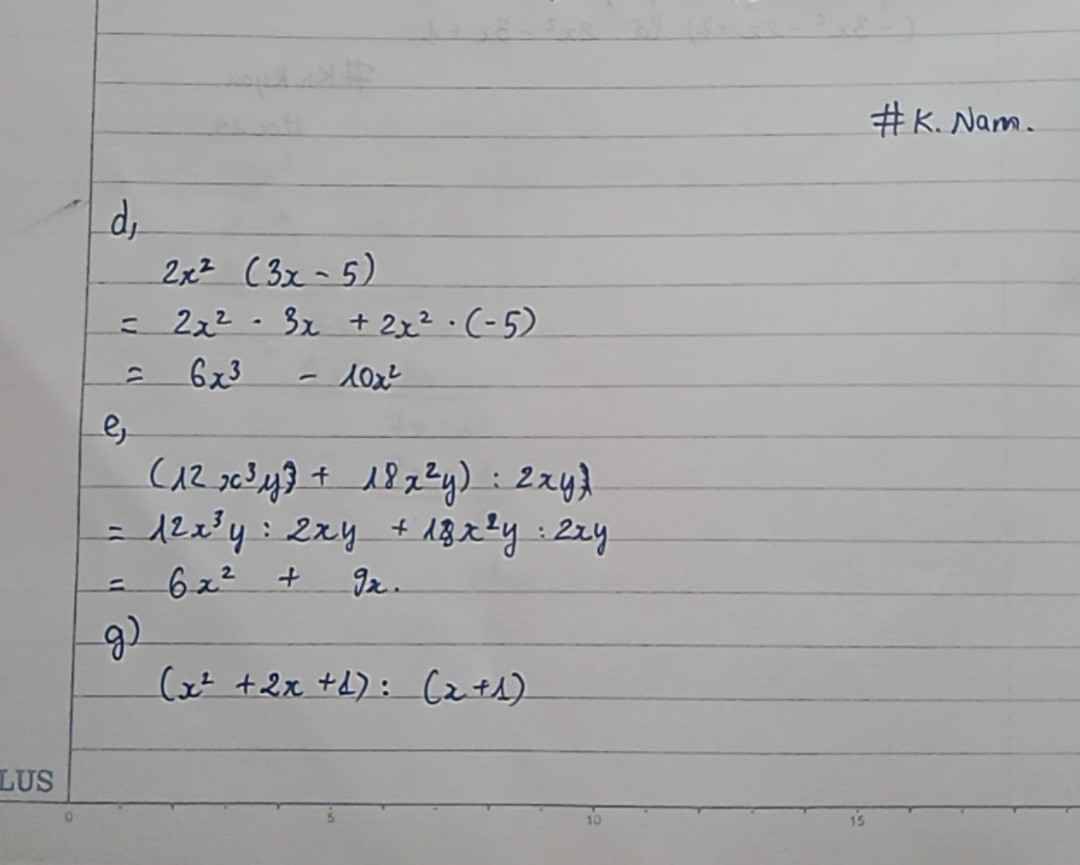

*Máy tớ cam hơi mờ, cậu thông cảm ._.*
Cậu viết lại rõ đề câu c, nhé.
a) |5x - 1| - x = 2x + 3
<=> |5x - 1| = 2x + 3 + x
<=> |5x - 1| = 3x + 3
<=> 5x - 1 = 3x + 3 hoặc 5x - 1 = -(3x + 3)
5x - 1 - 3x = 3 5x - 1 + 3x = -3
2x - 1 = 3 8x - 1 = -3
2x = 3 + 1 8x = -3 + 1
2x = 4 8x = -2
x = 2 x = -2/8 = -1/4
=> x = 2 hoặc x = -1/4
b) Ta có: |2x + 1| \(\ge\)0 \(\forall\)x
|x - 3| \(\ge\)0 \(\forall\)x
|2x+ 3| \(\ge\)0 \(\forall\)x
=> |2x + 1| + |x - 3| + |2x + 3| \(\ge\)0 \(\forall\)x
=> x - 5 \(\ge\)0 \(\forall\)x => x \(\ge\)5 \(\forall\)x
Với x \(\ge\)5
=> 2x + 1 + x - 3 + 2x + 3 = x - 5
=> 4x + 1 = x - 5
=> 4x - x = -5 - 1
=> 3x = -6
=> x = -2 (ktm)
Vậy ko có giá trị thõa mãn