
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(-2,6)*x+4,3*x-6,3=-4,6
(-2,6+4,3)*x-6,3=-4,6
1,7*x-6,3=-4,6
1,7*x=-4,6+6,3
1,7*x=1,7
x=1,7:1,7
x=1

Bài 5 :
a, ( -4,8 ) + \(\left[\left(-5,7\right)+\left(4,8\right)\right]\)
= (-4,8) + ( 4,8 ) + ( -5,7 )
= (-5,7 )
b) [(-9,6) + (+1,5)] + [(+9,6) + (-1,5)]
= (-9,6 ) + 9,6 + 1,5 + ( -1,5 )
= 0
c) (3,1 - 2,5) - (-2,5 + 3,1)
= 3,1 - 2,5 + 2,5 - 3,1
= 3,1 -3,1 -2,5 + 2,5
=0
= 3,1 - 2,5 + 2,5 + 3,1
= ( 3,1 - 3,1 ) + ( -2,5 - 2,5 )
= 0
d) 2,7 - (-4,3) + (-8,5) - (-0,6)
= 2,7 + 4,3 - 7 ,9
= 7 - 7,9
= -0,9
d) 2,7 - (-4,3) + (-8,5) - (-0,6)
= 2,7 + 4,3 + 8,5 + 0,6
= 7 + 9,1
= 16,1
e, - \(\left(\dfrac{3}{5}+\dfrac{3}{4}\right)-\left(\dfrac{3}{4}+\dfrac{2}{5}\right)\)
= \(\dfrac{-3}{5}+\dfrac{3}{4}-\dfrac{3}{4}-\dfrac{2}{5}\)
= \(\dfrac{-3}{5}-\dfrac{2}{5}+\dfrac{3}{4}-\dfrac{3}{4}\)
= -1
f) [(-4,9) + (-37,8)] + [(+1,9) + (+2,8)]
= - 4,9 - 37,8 + 1,9 + 2,8
= ( -4,9 + 1,9 ) + ( -37,8 + 2,8 )
= -3 + (-35)
= -38
g) (-4,1) + (-13,7) + (+31) + (-5,9) + (-6,3)
= (-4,1) + ( -5,9 ) + ( -13,7 ) + ( -6,3) + 31
= - 10 - 20 + 31
= 1
h) (-6,5) . 2,8 + 2,8 . (-3,5)
= 2,8 . [ -6,5 - 3,5 ]
= 2,8 . (-10 )
= - 28



a) A= 1,7+|3,4-x|
Ta thấy:\(\left|3,4-x\right|\ge0\)
\(\Rightarrow1,7+\left|3,4-x\right|\ge1,7+0=1,7\)
\(\Rightarrow A\ge1,7\)
Dấu = khi x=3,4
Vậy Amin=1,7 khi x=3,4
b) B= |x+2,8|-3,5
Ta thấy:\(\left|x+2,8\right|\ge0\)
\(\Rightarrow\left|x+2,8\right|-3,5\ge0-3,5=-3,5\)
\(\Rightarrow B\ge-3,5\)
Dấu = khi x=-2,8
Vậy Bmin=-3,5 khi x=-2,8
c) C= |4,3-x|+3,7
Ta thấy:\(\left|4,3-x\right|\ge0\)
\(\Rightarrow\left|4,3-x\right|+3,7\ge0+3,7=3,7\)
\(\Rightarrow C\ge3,7\)
Dấu = khi x=4,3
Vậy Cmin=3,7 khi x=4,3

Vì x và z tỉ lệ thuận với 3 và 4 => \(\frac{x}{3}=\frac{y}{4}\)(1)
Vì y và z tỉ lệ thuận với 5 và 7 => \(\frac{y}{5}=\frac{z}{7}\)(2)
Từ (1) và (2) => \(\frac{x}{3}=\frac{y}{4};\frac{y}{5}=\frac{z}{7}\)
+) \(\frac{x}{3}=\frac{y}{4}\Rightarrow\frac{x}{15}=\frac{y}{20}\)
\(\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{y}{20}=\frac{z}{28}\)
=> \(\frac{x}{15}=\frac{y}{20}=\frac{z}{28}\)
=> \(\frac{2x}{30}=\frac{3y}{60}=\frac{z}{28}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\frac{2x}{30}=\frac{3y}{60}=\frac{z}{28}=\frac{2x+3y-z}{30+60-28}=\frac{36}{62}=\frac{18}{31}\)
=> x = 18/31 .15 = 270/31
y = 18/31.20 = 360/31
z = 18/31.28 = 504/31
x,z tỉ lệ thuận với 3, 4
=> \(\frac{x}{3}=\frac{z}{4}\)(1)
y, z tỉ lệ thuận với 5, 7
=> \(\frac{y}{5}=\frac{z}{7}\)(2)
và 2x + 3y - z = 36 (3)
Từ (1), (2) và (3)
=> \(\hept{\begin{cases}\frac{x}{3}=\frac{z}{4}\\\frac{y}{5}=\frac{z}{7}\\2x+3y-z=36\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{x}{3}\times\frac{1}{7}=\frac{z}{4}\times\frac{1}{7}\\\frac{y}{5}\times\frac{1}{4}=\frac{z}{7}\times\frac{1}{4}\\2x+3y-z=36\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{x}{21}=\frac{z}{28}\\\frac{y}{20}=\frac{z}{28}\\2x+3y-z=36\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{x}{21}=\frac{y}{20}=\frac{z}{28}\\2x+3y-z=36\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{2x}{42}=\frac{3y}{60}=\frac{z}{28}\\2x+3y-z=36\end{cases}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{42}=\frac{3y}{60}=\frac{z}{28}=\frac{2x+3y-z}{42+60-28}=\frac{36}{74}=\frac{18}{37}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{18}{37}\cdot21=\frac{378}{37}\\y=\frac{18}{37}\cdot20=\frac{360}{37}\\z=\frac{18}{37}\cdot28=\frac{504}{37}\end{cases}}\)

a, \(\left|2x-3\right|-\dfrac{1}{3}=0\Leftrightarrow\left|2x-3\right|=\dfrac{1}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=\dfrac{1}{3}\\2x-3=-\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
b, tương tự
c, \(\left|2x-1\right|-\left|x+\dfrac{1}{3}\right|=0\Leftrightarrow\left|2x-1\right|=\left|x+\dfrac{1}{3}\right|\)
TH1 : \(2x-1=x+\dfrac{1}{3}\Leftrightarrow x=\dfrac{4}{3}\)
TH2 : \(2x-1=-x-\dfrac{1}{3}\Leftrightarrow3x=\dfrac{2}{3}\Leftrightarrow x=\dfrac{2}{9}\)
d, \(3x-\left|x+15\right|=\dfrac{5}{4}\Leftrightarrow\left|x+15\right|=3x-\dfrac{5}{4}\)ĐK : x >= 5/12
TH1 : \(x+15=3x-\dfrac{5}{4}\Leftrightarrow-2x=-\dfrac{65}{4}\Leftrightarrow x=\dfrac{65}{8}\)( tm )
TH2 : \(x+15=\dfrac{5}{3}-3x\Leftrightarrow4x=-\dfrac{40}{3}\Leftrightarrow x=-\dfrac{10}{3}\)
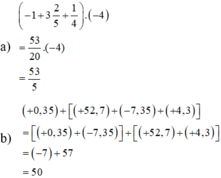
Ta có: \(A=4.3-13.5-5.7-6.3+\left|11.4-3.4\right|\)
\(=-2-13.5-5.7+8\)
\(=-13,2\)