H
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
17 tháng 12 2023
a) x³y + x - y - 1
= (x³y - y) + (x - 1)
= y(x³ - 1) + (x - 1)
= y(x - 1)(x² + x + 1) + (x - 1)
= (x - 1)[y(x² + x + 1) + 1]
= (x - 1)(x²y + xy + y + 1)
b) x²(x - 2) + 4(2 - x)
= x²(x - 2) - 4(x - 2)
= (x - 2)(x² - 4)
= (x - 2)(x - 2)(x + 2)
= (x - 2)²(x + 2)
c) x³ - x² - 20x
= x(x² - x - 20)
= x(x² + 4x - 5x - 20)
= x[(x² + 4x) - (5x + 20)]
= x[x(x + 4) - 5(x + 4)]
= x(x + 4)(x - 5)
d) (x² + 1)² - (x + 1)²
= (x² + 1 - x - 1)(x² + 1 + x + 1)
= (x² - x)(x² + x + 2)
= x(x - 1)(x² + x + 2)
KV
17 tháng 12 2023
e) 6x² - 7x + 2
= 6x² - 3x - 4x + 2
= (6x² - 3x) - (4x - 2)
= 3x(2x - 1) - 2(2x - 1)
= (2x - 1)(3x - 2)
f) x⁴ + 8x² + 12
= x⁴ + 2x² + 6x² + 12
= (x⁴ + 2x²) + (6x² + 12)
= x²(x² + 2) + 6(x² + 2)
= (x² + 2)(x² + 6)
g) (x³ + x + 1)(x³ + x) - 2
Đặt u = x³ + x
x³ + x + 1 = u + 1
(u + 1).u - 2
= u² + u - 2
= u² - u + 2u - 2
= (u² - u) + (2u - 2)
= u(u - 1) + 2(u - 1)
= (u - 1)(u + 2)
= (x³ + x - 1)(x³ + x + 2)
= (x³ + x - 1)(x³ + x² - x² - x + 2x + 2)
= (x³ + x - 1)[(x³ + x²) - (x² + x) + (2x + 2)]
= (x³ + x - 1)[x²(x + 1) - x(x + 1) + 2(x + 1)]
= (x³ + x - 1)(x - 1)(x² - x + 2)
h) (x + 1)(x + 2)(x + 3)(x + 4) - 1
= [(x + 1)(x + 4)][(x + 2)(x + 3)] - 1
= (x² + 5x + 4)(x² + 5x + 6) - 1 (1)
Đặt u = x² + 5x + 4
u + 2 = x² + 5x + 6
(1) u.(u + 2) - 1
= u² + 2u - 1
= u² + 2u + 1 - 2
= (u² + 2u + 1) - 2
= (u + 1)² - 2
= (u + 1 + √2)(u + 1 - √2)
= (x² + 5x + 4 + 1 + √2)(x² + 5x + 4 + 1 - √2)
= (x² + 5x + 5 + √2)(x² + 5x + 5 - √2)
PT
1
VT
2
TA
17 tháng 7 2021
a) `(x^3-x^2)/(x^3-2x^2+x)`
`=(x^2(x-1))/(x(x-1)(x-1))`
`=x/(x-1)`
`=>` 2 phân thức bằng nhau.
b) `(x^2+2x+1)/(2x^2-2)`
`=((x+1)(x+1))/(2(x+1)(x-1))`
`=(x+1)/(2(x-1))`
`=(x+1)/(2x-2)`
`=>` 2 phân thức bằng nhau
17 tháng 7 2021
a) Ta có: \(\dfrac{x^3-x^2}{x^3-2x^2+x}\)
\(=\dfrac{x^2\left(x-1\right)}{x\left(x^2-2x+1\right)}\)
\(=\dfrac{x\cdot\left(x-1\right)}{\left(x-1\right)^2}=\dfrac{x}{x-1}\)
b) Ta có: \(\dfrac{x^2+2x+1}{2x^2-2}\)
\(=\dfrac{\left(x+1\right)^2}{2\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{x+1}{2x-2}\)
18 tháng 7 2021
e) Ta có: \(x^4-2x^3+2x-1\)
\(=\left(x^4-1\right)-2x\left(x^2-1\right)\)
\(=\left(x^2+1\right)\left(x-1\right)\left(x+1\right)-2x\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x+1\right)\cdot\left(x^2-2x+1\right)\)
\(=\left(x+1\right)\cdot\left(x-1\right)^3\)
h) Ta có: \(3x^2-3y^2-2\left(x-y\right)^2\)
\(=3\left(x^2-y^2\right)-2\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
18 tháng 7 2021
a) Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
b) Ta có: \(x^2\left(x+2y\right)-x-2y\)
\(=\left(x+2y\right)\left(x^2-1\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)
24 tháng 9 2021
\(a,=\left(x-1\right)^3\\ b,=\left(1-2x\right)\left(1+2x\right)\\ c,=x^3-8\\ d,=\left(3x-1\right)\left(9x^2+3x+1\right)\\ e,=\left(x+2\right)\left(x^2-2x+4\right)\\ g,=\left(x-2\right)^2\\ h,=x^2-4y^2\\ j,=\left(x-4\right)^2\)
30 tháng 9 2021
\(A=6x^2+23x+21-\left(6x^2+23x-55\right)=76\\ B=x^4+x^3-x^2-2x^2-2x+2-x^4-x^3+3x^2+2x\\ =2\\ C=x^4+x^3-3x^2-2x-\left(x^4+x^3-x^2-2x^2-2x+2\right)\\ =-2\)
2 tháng 11 2021
Bài 1:
a) \(\Rightarrow3x^2+3x-2x^2-4x+x+1=0\)
\(\Rightarrow x^2=-1\left(VLý\right)\Rightarrow S=\varnothing\)
b) \(\Rightarrow\left(x-2020\right)\left(2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2020\\x=\dfrac{1}{2}\end{matrix}\right.\)
c) \(\Rightarrow\left(x-10\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=10\\x=-2\end{matrix}\right.\)
d) \(\Rightarrow\left(x+4\right)^2=0\Rightarrow x=-4\)
e) \(\Rightarrow\left(x+6\right)\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=7\end{matrix}\right.\)
f) \(\Rightarrow\left(5x-4\right)\left(5x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Bài 2:
a) \(\Rightarrow3x\left(x^2-4\right)=0\Rightarrow3x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
b) \(\Rightarrow x\left(x-2\right)+5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)
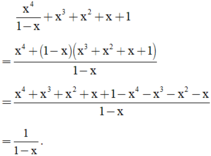
a) \(\frac{1}{x^2-x+1}+1-\frac{x^2+2}{x^3+1}\)
+) Đkxđ: \(\hept{\begin{cases}x^2-x+1\ne0\\x^3+1\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x^2-2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}\ne0\\x^3\ne-1\end{cases}\Leftrightarrow}\hept{\begin{cases}\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ne0\left(lđ\right)\\x\ne-1\end{cases}}}\)
+) \(A=\frac{1}{x^2-x+1}+1-\frac{x^2+2}{x^3+1}\)
\(=\frac{1}{x^2-x+1}+1-\frac{x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{x+1+x^3+1-x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{x^3-x^2+x+4}{\left(x+1\right)\left(x^2-x+1\right)}\)
P/s: ko chắc
Huhu luoi qua
a) \(\frac{1}{x^2-x+1}+1-\frac{x^2+2}{x^3+1}\)
\(=\frac{1}{x^2-x+1}+1-\left(\frac{x^2+2}{x^3+1}\right)\)
\(=\frac{x^5-2x^4+3x^3-2x^2+x}{x^5-x^4+x^3+x^2-x+1}\)
\(=\frac{x\left(x^4-2x^3+3x^2-2x+1\right)}{\left(x+1\right)\left(x^4-2x^3+3x^2-2x+1\right)}\)
\(=\frac{x}{x+1}\)
b) \(\frac{7}{x}-\frac{x}{x+6}+\frac{36}{x^2+6x}\)
\(=\frac{-x^2+7x+78}{x^2+6x}\)
\(=\frac{\left(-x-6\right)\left(x-13\right)}{x\left(x+6\right)}\)
\(=\frac{-x+13}{x}\)