Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Vì tích trên có đúng 100 số => 100 - n là thừa số thứ 100 => n = 100
\(\Rightarrow A=\left(100-1\right)\left(100-2\right)\left(100-3\right).....\left(100-100\right)=0\)
b ) \(B=13a+19b+4a-2b\)
\(=\left(13a+4a\right)+\left(19b-2b\right)\)
\(=17a+17b\)
\(=17\left(a+b\right)\)
\(=17.100=1700\)

3.
x={0 ;1;2 ;3 ;4 ;5 ;6 ;7........................}
ƯC(100;500) =100
suy ra x =100
BC(10;25) =50
suy ra x =50
tick nha

Lời giải:
$(x+1)+(x+2)+(x+3)+...+(x+100)=(1-x)+(2-x)+(3-x)+...+(100-x)$
$\underbrace{(x+x+...+x)}_{100}+(1+2+3+...+100)=(1+2+3+...+100)-\underbrace{(x+x+...+x)}_{100}$
$\Rightarrow 100x=-100x$
$\Rightarrow 200x=0$
$\Rightarrow x=0$

\(P=\dfrac{\left(1+2+3+...+100\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{9}\right)\left(63\cdot1,2-21\cdot3,6\right)}{1-2+3-4+5-6+...+99-100}\)
đề là vậy nhé mn
để ý chút thấy liền ah : 63.1,2-21.3,6=63.1,2-21.3.1,2= 63.1,2- 63.1,2=0
=============================
Ta có P = \(\dfrac{\left(1+2+3+...+100\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{9}\right)\left(63.1,2-21.3,6\right)}{1-2+3-4+5-...+99-100}\)= \(\dfrac{\left(1+2+3+...+100\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{9}\right)0}{1-2+3-4+5-...+99-100}\)= \(\dfrac{0}{1-2+3-4+5-6+...+99-100}=0\)

1. Để \(A_{min}\)thì \(x^4_{min}\)và \(2.x^2_{min}\) => \(x_{min}\) => \(x=0\)
Thay x vào ta có:\(A_{min}=0^4+2.0^2-7\)
\(A_{min}=0+0-7\)
\(A_{min}=-7\)
2. Ta có điểm M(1;5) => y=5;x=1
Thay x=1;y=5 vào ta có: \(5=a.1\)
=> a=5
4. Ta có: \(\frac{4x-9}{3x+y}-\frac{4y+9}{3y+x}=\frac{4x-\left(x-y\right)}{3x+y}-\frac{4y+\left(x-y\right)}{3y+x}\)
\(=\frac{4x-x+y}{3x+y}-\frac{4y+x-y}{3y+x}\)
\(=\frac{3x+y}{3x+y}-\frac{3y+x}{3y+x}\)
\(=1-1\)
\(=0\)
ban co bi gi ko lam thi phai cho mot it $ chu neu ko con lau ma lam cho

Ta có số trung bình cộng của các giá trị trong bảng là:
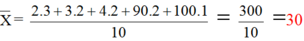
Trong trường hợp này không nên dùng số trung bình cộng làm đại diện cho dấu hiệu vì các giá trị của dấu hiệu chênh lệch đối với nhau quá lớn.