K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KK
1
DX
17 tháng 12 2022
11)\(\dfrac{3x+1}{x-5}+\dfrac{2x}{x-5}=\dfrac{3x+2x+1}{x-5}=\dfrac{5x+1}{x-5}\)
12)\(\dfrac{4-x^2}{x-3}+\dfrac{2}{x^2-9}=\dfrac{4-x^2}{x-3}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(4-x^2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{2+\left(2-x\right)\left(2+x\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
13)
\(\dfrac{3}{4x-2}+\dfrac{2x}{4x^2-1}=\dfrac{3}{2\left(2x-1\right)}+\dfrac{2x}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{3\left(2x+1\right)}{2\left(2x-1\right)\left(2x+1\right)}+\dfrac{2.2x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{6x+3+4x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{10x+3}{2\left(2x-1\right)\left(2x+1\right)}\)
14)
\(\dfrac{2x+1}{2x-4}+\dfrac{5}{x^2-4}=\dfrac{2x+1}{2\left(x-2\right)}+\dfrac{5}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x+1\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\dfrac{5.2}{2\left(x-2\right)\left(x+2\right)}=\dfrac{2x^2+5x+12}{2\left(x-2\right)\left(x+2\right)}\)
HK
1
VE
1
15 tháng 1 2022
Cách 1: \(5x^2-60x-5600=0\)\(\Leftrightarrow x^2-12x-1120=0\)\(\Leftrightarrow x^2-40x+28x-1120=0\)
\(\Leftrightarrow x\left(x-40\right)+28\left(x-40\right)=0\)\(\Leftrightarrow\left(x-40\right)\left(x+28\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x-40=0\\x+28=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=40\\x=-28\end{cases}}\)
Vậy \(\orbr{\begin{cases}x=40\\x=-28\end{cases}}\)
Cách 2: \(5x^2-60x-5600=0\)\(\Leftrightarrow x^2-12x-1120=0\)\(\Leftrightarrow x^2-2x.6+6^2-1156=0\)
\(\Leftrightarrow\left(x-6\right)^2-34^2=0\)\(\Leftrightarrow\left(x-6-34\right)\left(x-6+34\right)=0\)
\(\Leftrightarrow\left(x-40\right)\left(x+28\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x-40=0\\x+28=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=40\\x=-28\end{cases}}\)
Vậy \(\orbr{\begin{cases}x=40\\x=-28\end{cases}}\)
W
1
LX
26 tháng 3 2020
DKXD : x khac -1
\(\frac{-x}{x+1}\)+ 3 =\(\frac{2x+3}{x+1}\)
<=> \(\frac{-x}{x+1}\)+\(\frac{3\left(x+1\right)}{x+1}\)= \(\frac{2x+3}{x+1}\)
=> -x + 3x +3 = 2x +3
<=> 2x -2x =3-3
<=> 0x=0
<=> x=0(TMDK)
AB
0
G
2 tháng 7 2019
Đề thiếu ko nhỉ? cộng b^2 nữa chứ
\(\left(a-b\right)\left(a-2b\right)\left(a-3b\right)\left(a-4b\right)+b^2\)
\(=\left[\left(a-b\right)\left(a-4b\right)\right]\left[\left(a-2b\right)\left(a-3b\right)\right]+b^2\)
\(=\left(a^2-4ab-ab+4b^2\right)\left(a^2-3ab-2ab+6b^2\right)+b^2\)
\(=\left(a^2-5ab+4b^2\right)\left(a^2-5ab+6b^2\right)+b^2=\left(a^2-5ab+5b^2\right)^2-b^2+b^2\)
\(=\left(a^2-5ab+b^2\right)^2\rightarrowđpcm\)
KK
mong mọi nngười giúp ạ em đang cần gấp
2
29 tháng 10 2021
Vì P,Q là trung điểm HI,HK nên PQ là đtb tg HIK
Do đó \(PQ=\dfrac{1}{2}IK=9\left(cm\right)\)
29 tháng 10 2021
xét \(\Delta HIK\) có:
\(HP=IP\)\(\left(gt\right)\)
\(HQ=QK\left(gt\right)\)
\(\Rightarrow PQ\) là đường trung bình
\(\Rightarrow PQ=\dfrac{IK}{2}=\dfrac{18}{2}=9\left(cm\right)\)
8 tháng 7 2019
Góc C = 180 - 130 = 50
Góc B = 360 - (80+120+50) =110
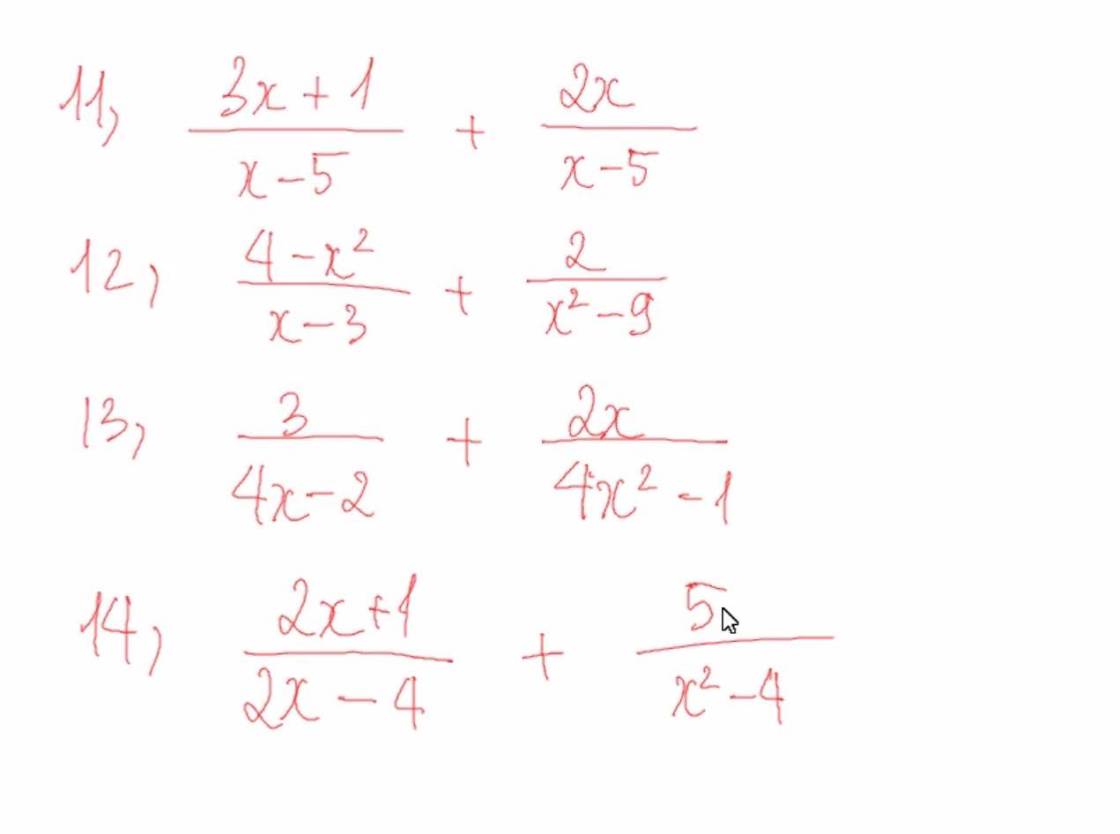
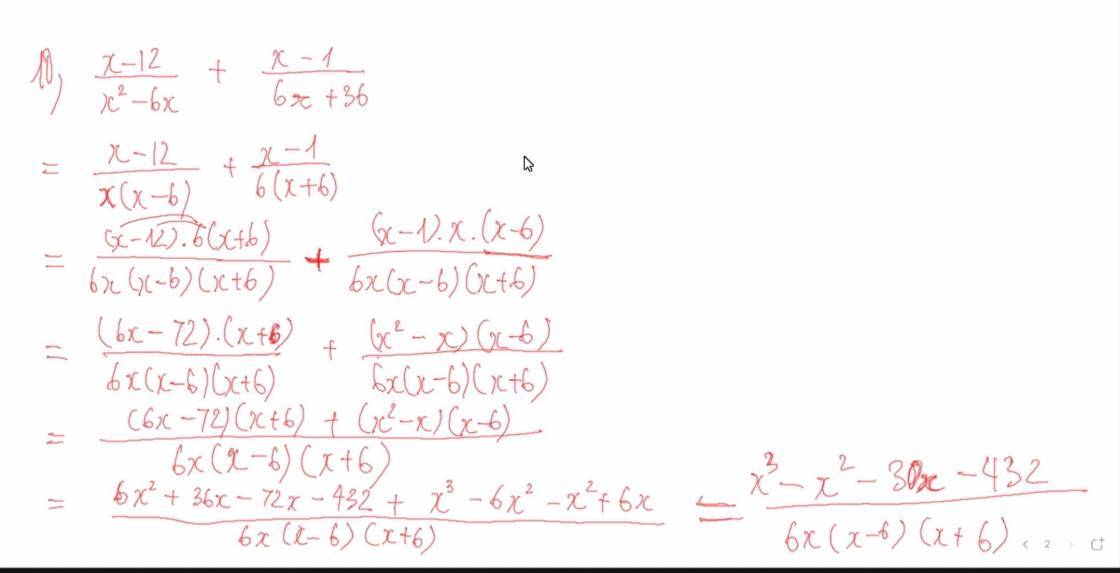
9(x5)2 = 4(x4)2
<=> (3.x5)2 = (2.x4)2
<=> 3x5 = 2x4
<=> 3x5 - 2x4 = 0
<=> x4(3x - 2) = 0
<=> \(\left[{}\begin{matrix}x^4=0\\3x-2=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
\(9x^{10}=4x^8\)
\(9x^{10}-4x^8=0\)
\(x^8\left(9x^2-4\right)=0\)
\(9x^2-4=0\)
\(x^2=\dfrac{4}{9}\)
⇒\(\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)