Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a)
Vì tam giác $ABC$ cân tại $A$ nên trung tuyến $AM$ đồng thời là đường cao. Do đó \(AM\perp BC\)
Xét tứ giác $AMNE$ có: \(\widehat{AME}=90^0=\widehat{ANE}\) và cùng nhìn cạnh $AE$ nên $AMNE$ là tứ giác nội tiếp.
Xét tứ giác $CMFN$ có tổng hai góc đối nhau \(\widehat{CMF}+\widehat{CNF}=90^0+90^0=180^0\) nên $CMFN$ là tứ giác nội tiếp.
* Xác định tâm.
Sử dụng tính chất: Đường trung tuyến ứng với cạnh huyền trong tam giác vuông thì bằng một nửa cạnh huyền.
Gọi $I$ là trung điểm của $AE$.
Xét tam giác $AME$ vuông tại $M$ có đường trung tuyến ứng với cạnh huyền là $MI$ nên \(MI=\frac{AE}{2}=AI=EI\)
Xét tam giác $ANE$ vuông tại $N$ có đường trung tuyến ứng với cạnh huyền là $NI$ nên \(NI=\frac{AE}{2}=AI=EI\)
Do đó: \(MI=NI=AI=EI\) nên $I$ là tâm đường tròn ngoại tiếp tứ giác $AMNE$.
Hoàn toàn tương tự, gọi $T$ là trung điểm $CF$ thì $T$ cũng là tâm đường tròn ngoại tiếp tứ giác $CMFN$
b)
Ta có:
\(\widehat{AEB}=90^0-\widehat{ABE}=90^0-\widehat{ABC}\)
\(\widehat{FEB}=90^0-\widehat{EFM}=90^0-\widehat{ACB}\) ( tứ giác $CMFN$ nội tiếp nên \(\widehat{EFM}=\widehat{ACB}\))
Mà \(\widehat{ABC}=\widehat{ACB}\) (do tam giác $ABC$ cân tại $A$)
\(\Rightarrow \widehat{AEB}=\widehat{FEB}\). Suy ra $EB$ là phân giác góc $\widehat{AEF}$
c) Xét tam giác $AEF$ có $EM$ vừa là đường cao, vừa là đường phân giác (phần b) nên $AEF$ là tam giác cân tại $E$
\(\Rightarrow EM\) đồng thời cũng là đường trung tuyến. Do đó $M$ là trung điểm của $AF$
Xét tam giác $ANF$ vuông tại $N$ có trung tuyến $NM$ ứng với cạnh huyền nên \(NM=\frac{AF}{2}=AM=MF\)
Suy ra $M$ là tâm đường tròn ngoại tiếp tam giác $AFN$

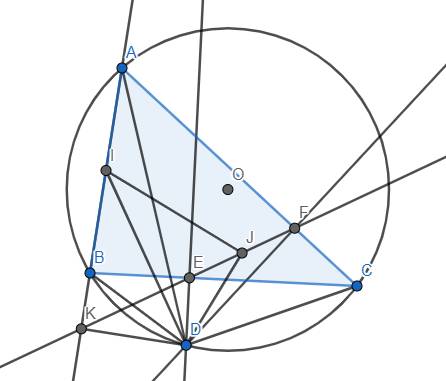
a) Theo đề bài, ta có \(\widehat{DEC}=\widehat{DFC}=90^o\) \(\Rightarrow\) Tứ giác CDEF nội tiếp do có 2 đỉnh kề nhau E, F cùng nhìn cạnh CD dưới góc vuông. \(\Rightarrow\widehat{DFE}=\widehat{DCE}=\widehat{DCB}=\widehat{DAB}\) (do tứ giác ABDC nội tiếp nên \(\widehat{DCB}=\widehat{DAB}\)). Từ đó suy ra đpcm.
b) Có \(\widehat{KBD}=\widehat{ACD}\) (do tứ giác ABDC nội tiếp) và \(\widehat{ACD}=\widehat{KED}\) (do tứ giác CDEF nội tiếp) \(\Rightarrow\widehat{KBD}=\widehat{KED}\) \(\Rightarrow\) Tứ giác DKBE nội tiếp.
Mặt khác, \(\widehat{BDA}=\widehat{BCA}=\widehat{EDF}\) và \(\widehat{BAD}=\widehat{BCD}=\widehat{EFD}\)
\(\Rightarrow\Delta DBA~\Delta DEF\left(g.g\right)\)\(\Rightarrow\dfrac{DA}{DF}=\dfrac{DB}{DE}\) \(\Rightarrow DA.DE=DB.DF\)
c) \(\Delta DBA~\Delta DEF\Rightarrow\dfrac{DB}{DE}=\dfrac{AB}{EF}=\dfrac{2BI}{2EJ}=\dfrac{BI}{EJ}\) . Lại có \(\widehat{DBI}=\widehat{DEJ}\) nên \(\Delta DBI~\Delta DEJ\left(c.g.c\right)\) \(\Rightarrow\widehat{DIB}=\widehat{DJE}\) hay \(\widehat{DIK}=\widehat{DJK}\) \(\Rightarrow\) Tứ giác DJIK nội tiếp \(\Rightarrow\) \(\widehat{DJI}=180^o-\widehat{DKI}\) . Lại có \(\widehat{DKI}=180^o-\widehat{BED}=90^o\) (do tứ giác DKBE nội tiếp) \(\Rightarrow\widehat{DJI}=90^o\) \(\Rightarrow\) đpcm

là sao
lưu ý cấm hs đăng những câu hỏi linh tinh ko liên quan đến toán
đúng bạn phạm nội quy online math