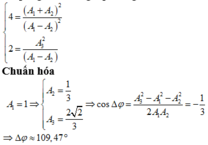Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Dao động tổng hợp hai dao động có biên độ A 1 – A 2 → hai dao động ngược pha nhau. Độ lệch pha giữa chúng là k = 0 , ± 1 , ± 2... với

+ Ta có
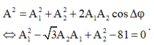
Để phương trình trên tồn tại nghiệm A 1 thì
![]()
Thay giá trị A 2 vào phương trình đầu, ta tìm được
![]()
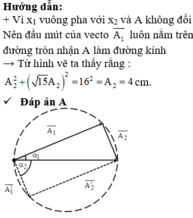
Đáp an A


\(\overrightarrow{A}=\overrightarrow{A_1}+\overrightarrow{A_2}\)
Định lý hàm sin: \(\dfrac{A}{\sin\dfrac{\pi}{6}}=\dfrac{A_2}{\sin\alpha}=\dfrac{A_1}{\sin\beta}\)
\(A_2\left(max\right)\Rightarrow\sin\alpha_{max}=1\Rightarrow\left\{{}\begin{matrix}A_2=\dfrac{9}{\dfrac{1}{2}}=18\left(cm\right)\\\alpha=\dfrac{\pi}{2}\left(rad\right)\end{matrix}\right.\)
\(\Rightarrow\beta=\pi-\dfrac{\pi}{6}-\dfrac{\pi}{2}=\dfrac{\pi}{3}\left(rad\right)\Rightarrow A_1=18.\sin\dfrac{\pi}{3}=9\sqrt{3}\left(cm\right)\)

Đáp án B
Phương pháp :Sử dụng công thức tính biên độ dao động tổng hợp hai dao động cùng phương, cùng tần số
Khi đó dao động tổng hợp được xác định bởi biểu thức :
A = A 1 2 + A 2 2 + 2 A 1 A 2 cos ∆ φ ; ∆ φ = π 2 ⇒ A = A 1 2 + A 2 2


![]()
![]()
Bình luận: Để nhanh chóng tìm được kết quả ta chuẩn hóa nhanh như sau
*Lập tỉ giữa 2 trong 3 phương trình trên ta được: