VT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KN
20 tháng 6 2019
1a) \(\frac{5}{1,2}=\frac{-2,5}{x}\)
\(\Leftrightarrow5x=-3\)
\(\Leftrightarrow x=\frac{-3}{5}\)
b) \(\frac{3,2+\left(-0,4\right)}{-x-3,6}=\frac{-0,75}{1,5}\)
\(\Leftrightarrow\frac{2,8}{-x-3,6}=\frac{-0,75}{1,5}\)
\(\Leftrightarrow4,2=0,75x+2,7\)
\(\Leftrightarrow0,75x=1,5\)
\(\Leftrightarrow x=2\)
2) \(\frac{1}{3}.\frac{5}{7}=\frac{2}{7}.\frac{5}{6}\)
Tỉ lệ thức lập được \(\frac{5}{21}=\frac{10}{42}\)
2 tháng 3 2020
\(2^x:1+2^x:2+...+2^x:49=2^{49}-1\)
\(2^x.1+2^x.\frac{1}{2}+...+2^x.\frac{1}{49}=2^{49}-1\)
\(2^x.\left(1+\frac{1}{2}+...+\frac{1}{49}\right)=2^{49}-1\)
3 tháng 3 2020
Đặt: \(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{49}}\)
=> \(2A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{48}}\)
=> \(2A-A=\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{48}}\right)-\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^{49}}\right)\)
=> \(A=1-\frac{1}{2^{49}}=\frac{2^{49}-1}{2^{49}}\)
\(2^{x-1}+2^{x-2}+2^{x-3}+...+2^{x-49}=2^{49}-1\)
<=> \(\frac{2^x}{2}+\frac{2^x}{2^2}+\frac{2^x}{2^3}+...+\frac{2^x}{2^{49}}=2^{49}-1\)
<=> \(2^x\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{49}}\right)=2^{49}-1\)
<=> \(2^x.\frac{2^{49}-1}{2^{49}}=2^{49}-1\)
<=> \(2^x=2^{49}\)
<=> x = 49.
E
14 tháng 12 2017
Chia cả hai vế cho 5^x:
pt <=> (3/5)^x + (4/5)^x = 1
- Ta nhận thấy x=2 là nghiệm của phương trình
(3/5)^2 + (4/5)^2 = 1
- Ta phải chứng minh x=2 là nghiệm duy nhất của phương trình
+ với x>2: (3/5)^x < (3/5)^2 (do 3/5 <1)
(4/5)^x < (4/5)^2 (do 4/5<1)
----------------------------------------...
Cộng 2 vế: (3/5)^x + (4/5)^x < (3/5)^2 + (4/5)^2 = 1 (trái gt)
=> Phương trình không có nghiệm khi x>2.
+ Tương tự với x<2, phương trình không có nghiệm khi x<2.
- Vậy phương trình có nghiệm duy nhất x=2.
14 tháng 12 2017
3^x+4^x=5^x vax=2
Thay x vao bieu thu ta co :
3^2+4^2=5^2
Xong roi do
30 tháng 9 2021
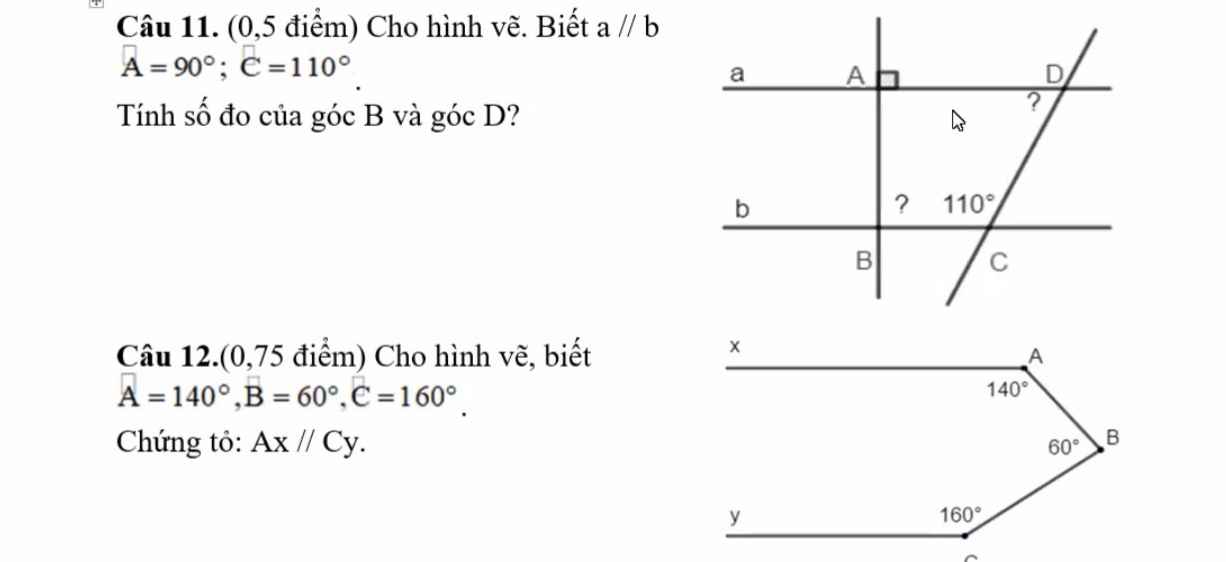
câu 11
có a// b mà a vuông góc với AB
=> b vuông góc với AB
=> góc B=90 độ
có góc D=1800-góc C
góc D= 1800-1100=700
MN
6
2 tháng 1
ta có 202220=(20222)10=408848410
Vì 4088484 < 20222022 nên 408848410<2022202210
Vậy 202220<2022202210
2 tháng 1
Rất dễ nhận thấy là 20222022 lớn hơn 2022 rất nhiều lần
\(\Rightarrow\)\(2022^{20}< 20222022^{10}\)
26 tháng 8 2021
a) \(x-\dfrac{1}{4}=-\dfrac{1}{6}\Leftrightarrow x=-\dfrac{1}{6}+\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{12}\)
b) \(\dfrac{2}{5}x-\dfrac{1}{9}=\left(\dfrac{1}{3}\right)^2\Leftrightarrow\dfrac{2}{5}x=\dfrac{1}{9}+\dfrac{1}{9}\Leftrightarrow\dfrac{2}{5}x=\dfrac{2}{9}\Leftrightarrow x=\dfrac{5}{9}\)
c) \(\left|x+\dfrac{1}{3}\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=3\\x+\dfrac{1}{3}=-3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3-\dfrac{1}{3}\\x=-3-\dfrac{1}{3}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=-\dfrac{10}{3}\end{matrix}\right.\)
26 tháng 8 2021
\(\left(a\right)\)
\(x-\dfrac{1}{4}=\dfrac{-1}{6}\)
\(x=\dfrac{1}{12}\)
/\(x+\dfrac{1}{3}\)/=3
=> \(x+\dfrac{1}{3}=3\) hoặc \(-x-\dfrac{1}{3}=3\)
=> x=\(\dfrac{8}{3}\) hoặc x= \(\dfrac{-10}{3}\)
2 tháng 9 2021
a) \(\dfrac{3}{7}+\left(-\dfrac{5}{2}\right)+\left(-\dfrac{3}{7}\right)=\dfrac{3}{7}-\dfrac{5}{2}-\dfrac{3}{7}=-\dfrac{5}{2}\)
b) \(B=\dfrac{4^2.2^3}{2^6}=\dfrac{\left(2^2\right)^2.2^3}{2^6}=\dfrac{2^4.2^3}{2^6}=\dfrac{2^7}{2^6}=2\)
5 tháng 1 2022
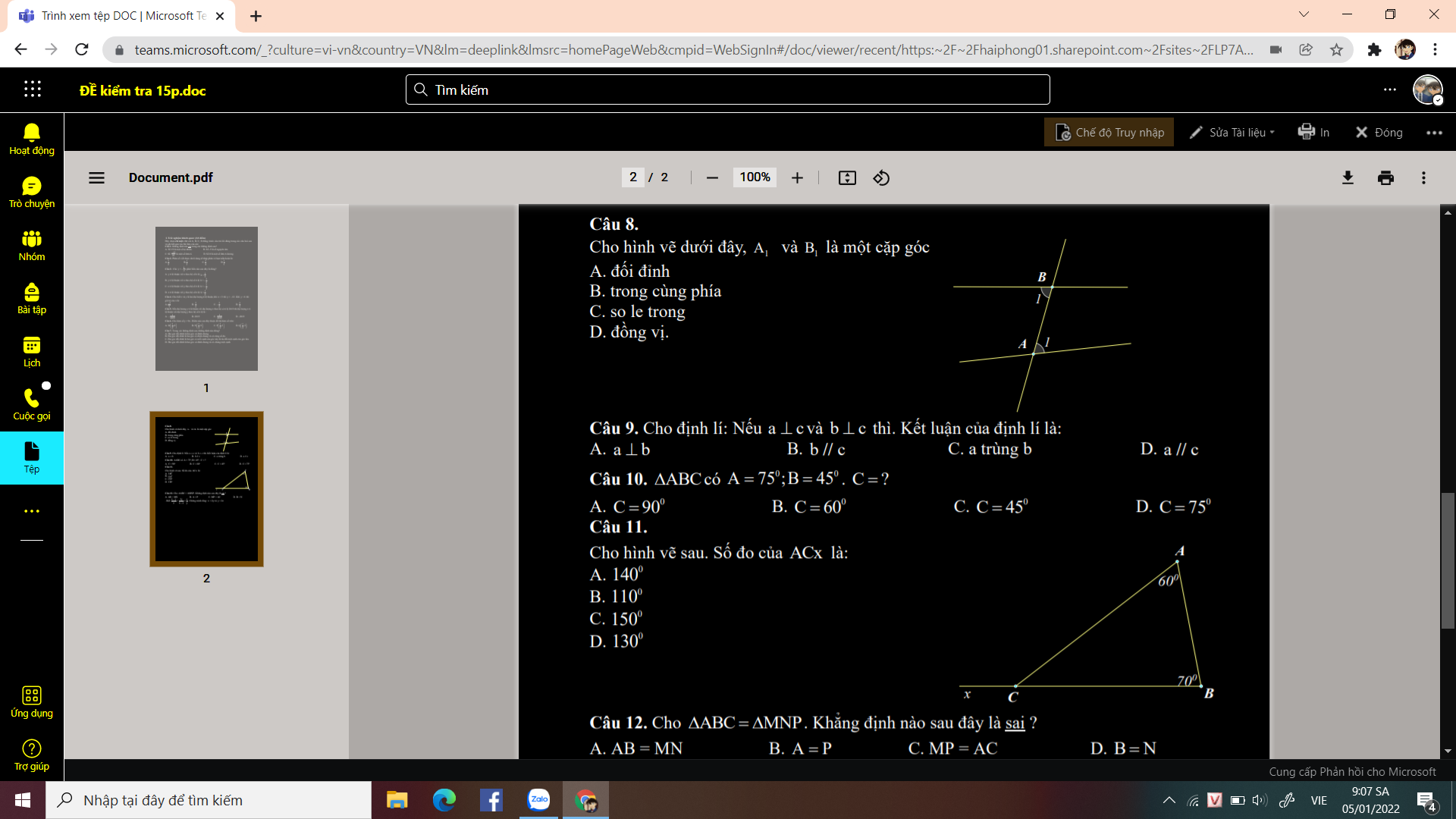
\(\text{8.C.So le trong}\)
\(\text{9.C.a trùng b}\)
\(\text{10.B.}60^0\)
\(\text{11.C.}150^0\)
\(\text{12.B.A=P}\)
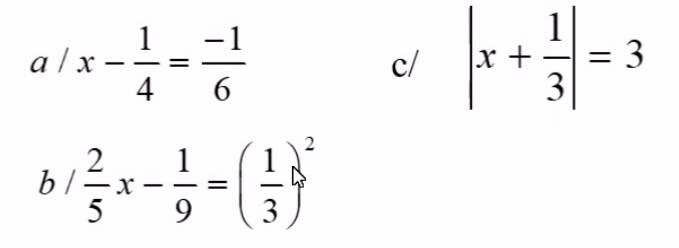
\(6,8x-3,6x-3,2=-9,6\)
\(3,2x=-9,6+3,2\)
\(3,2x=-6,4\)
\(x=-2\)
vậy \(x=-2\)
học tôt Vũ Trà My
có ai ko, giúp mk với