Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

46:
(SAB) và (SAD) cùng vuông góc (ABCD)
=>SA vuông góc (ABCD)
=>SA vuông góc AC
ΔSAC vuông tại A
=>\(SC=\sqrt{AS^2+AC^2}=a\sqrt{2}\)
\(V=\dfrac{1}{3}\cdot SA\cdot S_{ABCD}=\dfrac{1}{3}\cdot a\sqrt{2}\cdot a^2=\dfrac{a^3\sqrt{2}}{3}\)
=>Chọn C
47:
\(\dfrac{V_{BC.A'B'C'}}{V_{ABC.A'B'C'}}=\dfrac{2}{3}\)
=>V1=2/3*V
=>Chọn A
48:
AB vuông góc AC
AB vuông góc AD
Do đó: AB vuông góc (ACD)
\(V_{ABCD}=\dfrac{1}{3}\cdot AB\cdot S_{ACD}=\dfrac{1}{3}\cdot5\cdot\dfrac{1}{2}\cdot12\cdot10=100\)
=>Chọn A

a: Số số hạng là:
(40-2):2+1=20(số)
Tổng là:
\(\dfrac{42\cdot20}{2}=42\cdot10=420\)

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.


46.
Giả sử hình vuông ABCD tâm I, do I là tâm đối xứng hình vuông nên là tâm đối xứng đồ thị
\(\Rightarrow\) I là điểm uốn có tọa độ \(I\left(0;0\right)\) của hàm số
Do A đối xứng C, B đối xứng D qua I (đồng thời là gốc tọa độ) nên trong các cặp điểm AC và BD luôn có 2 điểm mang hoành độ dương và 2 điểm mang hoành độ âm, ko mất tính tổng quát, giả sử A và B mang hoành độ dương. Gọi \(A\left(a;a^3-3a\right)\) ; \(B\left(b;b^3-3b\right)\) với \(b>a>0\)
\(\Rightarrow C\left(-a;-a^3+3a\right)\) ; \(D\left(-b;-b^3+3b\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{CA}=\left(2a;2a^3-6a\right)\\\overrightarrow{DB}=\left(2b;2b^3-6b\right)\end{matrix}\right.\)
ABCD là hình vuông \(\Rightarrow\left\{{}\begin{matrix}AC=BD\\AC\perp BD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a^2+\left(a^3-3a\right)^2=b^2+\left(b^3-3b\right)^2\\ab+\left(a^3-3a\right)\left(b^3-3b\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2+a^2\left(a^2-3\right)^2=b^2+b^2\left(b^2-3\right)^2\\1+\left(a^2-3\right)\left(b^2-3\right)=0\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}a^2-3=x>-3\\b^2-3=y>-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x+3+x^2\left(x+3\right)=y+3+y^2\left(y+3\right)\\xy=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)\left(x^2+xy+y^2+3x+3y+1\right)=0\\xy=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2+3\left(x+y\right)+2=0\\xy=-1\end{matrix}\right.\) (do \(b>a>0\Rightarrow x\ne y\))
\(\Rightarrow\left[{}\begin{matrix}x+y=-1;xy=-1\\x+y=-2;xy=-1\end{matrix}\right.\)
Sử dụng Viet đảo ta được
\(\left(x;y\right)=\left(\dfrac{-1-\sqrt{5}}{2};\dfrac{-1+\sqrt{5}}{2}\right);\left(\dfrac{-1+\sqrt{5}}{2};\dfrac{-1-\sqrt{5}}{2}\right);\left(-1-\sqrt{2};-1+\sqrt{2}\right);\left(-1+\sqrt{2};-1-\sqrt{2}\right)\)
Do \(y>x\) nên chỉ có 2 cặp thỏa mãn. Mỗi giá trị x; y cho đúng 1 giá trị a; b dương tương ứng, nên có 2 cặp A; B thỏa mãn \(\Rightarrow\) có 2 hình vuông thỏa mãn (thực ra có thể tìm chính xác tọa độ A; B nhưng nó hơi xấu, ví dụ ứng với \(x=\dfrac{-1-\sqrt{5}}{2}\Rightarrow a^2=x+3=\dfrac{5-\sqrt{5}}{2}\Rightarrow a=\sqrt{\dfrac{5-\sqrt{5}}{2}}\) ko rút gọn được
47.
- Nhận xét quan trọng: hai mặt phẳng (a) và Oxy vuông góc (thấy ngay bằng dấu hiệu cả hai đều "khuyết z")
Từ nhận xét trên, ta thấy khoảng cách từ điểm H thuộc Oxy tới (a) chính là khoảng cách từ H tới d, với d là giao tuyến của (a) và mp Oxy.
Gọi K là hình chiếu vuông góc của M xuống Oxy \(\Rightarrow MK\perp Oxy\) với \(K\left(4;-2;0\right)\)
\(\Rightarrow MK\perp d\) ; mà \(d\perp MH\) theo giả thiết \(\Rightarrow d\perp\left(MHK\right)\)
\(\Rightarrow d\perp KH\) hay tam giác AHK vuông tại H
\(\Rightarrow\) Quỹ tích H là đường tròn đường kính AK thuộc mặt phẳng Oxy
Bây giở ta có 1 bài toán hình học phẳng đơn giản : cho 1 đường thằng cố định nằm ngoài đường tròn (O), tìm điểm M thuộc (O) sao cho khoảng cách từ M tới d đạt min. Lời giải đơn giản là qua tâm O đường tròn vẽ đường thẳng d' vuông góc d, d' cắt (O) tại A (với A nằm giữa O và d), khi đó khoảng cách từ A tới d sẽ ngắn nhất.
Trong bài toán này, để khỏi cần tính toán nhiều thì ta tính nhanh khoảng cách nhỏ nhất như sau:
Gọi I là trung điểm AK \(\Rightarrow I\left(1;2;0\right)\)
\(\Rightarrow d\left(H;\left(\alpha\right)\right)_{min}=d\left(I;\left(\alpha\right)\right)-\dfrac{AK}{2}\) (có biết tại sao có biểu thức này không?) \(=15\)

Lấy logarit cơ số 4 hai vế:
\(log_44^{log_57}=log_47^{log_54}\)
\(\Leftrightarrow log_57=log_54.log_47\)
\(\Leftrightarrow log_57=\frac{log_47}{log_45}\)
\(\Leftrightarrow log_57=log_57\)
Đẳng thức cuối cùng đúng, vậy ta có đpcm

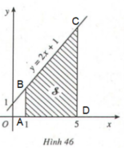
1. Kí hiệu A là điểm có tọa độ (1,0), D là điểm có tọa độ (5,0). B, C lần lượt là giao điểm của đường thẳng x = 1 và x = 5 với đường thẳng y = 2x + 1.
- Khi đó B và C sẽ có tọa độ lần lượt là (1,3) và (5,11).
- Ta có: AB = 3, CD = 11, AD = 4. Diện tích hình thang 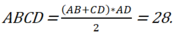
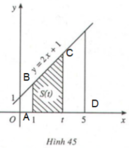
2. Kí hiệu A là điểm có tọa độ (1,0), D là điểm có tọa độ (5,0). B, C lần lượt là giao điểm của đường thẳng x = 1 và x = 5 với đường thẳng y = 2x + 1.
- Khi đó ta có B (1,3) và C(t, 2t + 1).
- Ta có AB = 3, AD = t – 1, CD = 2t + 1.
- Khi đó diện tích hình thang
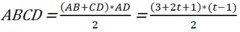
![]()


12313544657