
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: =>5x+25-3x+6=25+18
=>2x+41=43
=>2x=2
=>x=1
b: =>4x+8=3x+3+17
=>4x+8=3x+20
=>x=12
a: =>5x+25-3x+6=25+18
=>2x+41=43
=>2x=2
=>x=1
b: =>4x+8=3x+3+17
=>4x+8=3x+20
=>x=12

\(a.\dfrac{2}{3}+\dfrac{1}{5}\cdot\dfrac{10}{7}\\ =\dfrac{2}{3}+\dfrac{2}{7}=\dfrac{20}{21}\\ b.\dfrac{7}{12}-\dfrac{27}{7}\cdot\dfrac{1}{18}\\ =\dfrac{7}{12}-\dfrac{3}{14}=\dfrac{31}{84}\\ c.\left(\dfrac{23}{11}-\dfrac{15}{82}\right)\cdot\dfrac{41}{25}\\ =\dfrac{1721}{902}\cdot\dfrac{41}{25}=\dfrac{1721}{550}\\ d.\left(\dfrac{4}{5}+\dfrac{1}{2}\right)\cdot\left(\dfrac{3}{13}-\dfrac{8}{13}\right)\\ =\dfrac{13}{10}\cdot\left(\dfrac{-5}{13}\right)=\dfrac{-1}{2}\)

Bài giải
Ta có: 6n + 4 \(⋮\)2n + 1 (n \(\inℤ\))
=> 6n + 4 - 3(2n + 1) \(⋮\)2n + 1
=> 1 \(⋮\)2n + 1
=> 2n + 1 \(\in\)Ư (1)
Ư (1) = {1; -1}
2n + 1 = 1 hay -1
2n = 1 - 1 hay -1 - 1
2n = 0 hay -2
n = 0 : 2 hay -2 : 2
n = 0 hay -1
Vậy n = 0 hay -1

h: \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{9\cdot10}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=1-\dfrac{1}{10}=\dfrac{9}{10}\)
m: \(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
\(=\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
\(=\dfrac{1}{2}-\dfrac{1}{8}=\dfrac{3}{8}\)

\(25\%=\frac{1}{4}\)
Suy ra \(A=\frac{1}{4}-\frac{5}{4}-\frac{1}{\frac{5}{6}}=-1-\frac{6}{5}=-\frac{11}{5}\)

\(A=3+3^2+...+3^{2005}\)
\(\Rightarrow3A=3^2+3^3+...+3^{2006}\)
\(\Rightarrow3A-A=3^{2006}-3\)
\(\Rightarrow2A=3^{2006}-3\)
\(\Rightarrow2A+3=3^{2006}\) là 1 lũy thừa của 3 (đpcm)
4.
\(B=1+1+2+2^2+2^3+...+2^{100}\)
\(2B=2+2+2^2+...+2^{101}\)
\(\Rightarrow2B-B=2+2^{101}-\left(1+1\right)=2^{101}\)
\(\Rightarrow B=2^{101}\) là 1 lũy thừa của 2 (đpcm)

Bài 1:
\(A=2+2^2+2^3+...+2^{2003}+2^{2004}\)
\(=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{2002}+2^{2003}+2^{2004}\right)\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2002}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+2^4+...+2^{2002}\right)⋮7\)
Bài 2:
\(A=2+2^2+2^3+2^4+...+2^{59}+2^{60}\)
\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2\left(1+2+2^2+2^3\right)+2^5\left(1+2+2^2+2^3\right)+...+2^{57}\left(1+2+2^2+2^3\right)\)
\(=15\cdot\left(2+2^5+...+2^{57}\right)⋮15\)
Bài 3:
\(A=1+3+3^2+3^3+...+3^{1990}+3^{1991}\)
\(=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+...+\left(3^{1989}+3^{1990}+3^{1991}\right)\)
\(=13+3^3\left(1+3+3^2\right)+...+3^{1989}\left(1+3+3^2\right)\)
\(=13\left(1+3^3+...+3^{1989}\right)⋮13\)
Bài 4:
\(A=4+4^2+4^3+4^4+...+4^{23}+4^{24}\)
\(=\left(4+4^2\right)+\left(4^3+4^4\right)+...+\left(4^{23}+4^{24}\right)\)
\(=\left(4+4^2\right)+4^2\left(4+4^2\right)+...+4^{22}\left(4+4^2\right)\)
\(=20\left(1+4^2+...+4^{22}\right)⋮20\)
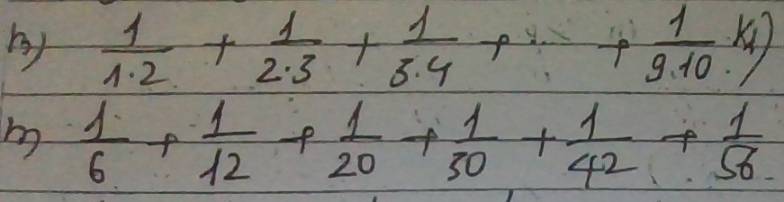 giúp em gấp phần m,n với ah cj ơi. Em cám ơn rấc nhìu ạa
giúp em gấp phần m,n với ah cj ơi. Em cám ơn rấc nhìu ạa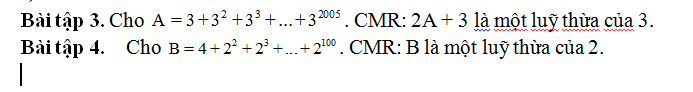

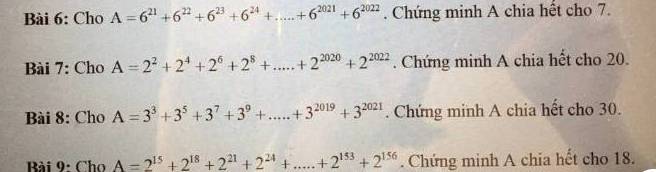


\(\left(-5\right).\dfrac{1}{3}=\dfrac{-5}{3}\)
=\(-\dfrac{5}{3}\)