
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


( 3x - 24 ) . 75 = 2.76 .1/20170
( 3x - 24 ) . 75 =235298
( 3x - 24 ) = 235298 : 75
( 3x - 24 ) =14
3x = 14 + 24
3x = 30
x = 0
dung 100%
\(\left(3x-2^4\right).7^5=2.7^6.\frac{1}{2017^0}\)
\(\Leftrightarrow\left(3x-16\right).7^5=2.7^6.1\)
\(\Leftrightarrow3x-16=\frac{2.7^6}{7^5}\)
\(\Leftrightarrow3x-16=2.7\)
\(\Leftrightarrow3x-16=14\)
\(\Leftrightarrow3x=30\)
\(\Leftrightarrow x=10\)

\(\left(\frac{1}{9}\right)^{2017}.9^{2017}-96^2:24^2=\left(3x-2\right)^3+12\)
\(\left(\frac{1}{9}.9\right)^{2017}-\left(96:24\right)^2=\left(3x-2\right)^3+12\)
\(1^{2017}-4^2=\left(3x-2\right)^3+12\)
\(-15=\left(3x-2\right)^3+12\)
\(\Rightarrow\left(3x-2\right)^3=-27\rightarrow3x-2=3\)
\(\Rightarrow x=\frac{5}{3}\)

\(\left(3x-7\right)^{2015}=\left(3x-7\right)^{2017}\Rightarrow\left(3x-7\right)^{2017}-\left(3x-7\right)^{2015}=0\Leftrightarrow\left(3x-7\right)^{2015}\left[\left(3x-7\right)^2-1\right]=0\Leftrightarrow\orbr{\begin{cases}3x-7=0\\\left(3x-7\right)^2=1\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}3x=7\\3x-7=1\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{3}\\x=\frac{1+7}{3}=\frac{8}{3}\end{cases}}\)
Vậy phương trình có hai nghiệm là \(x=\frac{7}{3}\)và \(x=\frac{8}{3}\)
Vì \(\left(3x-7\right)^{2015}=\left(3x-7\right)^{2017}\) =>3x-7=0 hoặc 3x-7=1
- Nếu 3x-7=0=>x=\(\frac{7}{3}\)
- Nếu 3x-7=1=>x=\(\frac{8}{3}\)
Vậy \(x=\orbr{\begin{cases}\frac{7}{3}\\\frac{8}{3}\end{cases}}\)

Nếu ở cuối là = 2013.1007 thì phương trình có nghiệm là x = 1 Vì:
Ta thực hiện thao tác nhóm như sau:
(x+2012x) + (2x+2011x) + (3x+2010x) + ....+ 2013x = 2013.1007
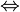 2013x + 2013x + 2013x + ...+ 2013x = 2013.1007
2013x + 2013x + 2013x + ...+ 2013x = 2013.1007
có tất cả 1006 số 2013x cộng với 2013x = 2013.1007
Vậy: 1006.2013x + 2013x = 2013.1007
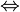 (1006 + 1)2013x = 2013.1007
(1006 + 1)2013x = 2013.1007 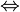 x = (2013.1007)/[(1006+1)2013] = 1
x = (2013.1007)/[(1006+1)2013] = 1

\(\left(-5-x\right)\left(3x+15\right)=\left(-2017\right)^{2008}\)
\(\Rightarrow-5\left(3x+15\right)-x\left(3x+15\right)=2017^{2008}\)
\(\Rightarrow-15x-75-3x^2+15x=2017^{2008}\)
\(\Rightarrow-75-3x^2=2017^{2008}\)
\(\Rightarrow3x^2=-75-2017^{2008}\)
\(3x^2\ge0\)
\(-75-2017^{2008}< 0\)
Vậy phương trình vô nghiệm