
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


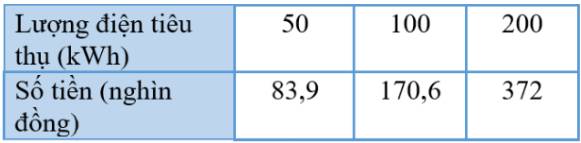
a) Số tiền phải trả tương ứng với lượng điện 50kWh là:
\(50.1,678 = 83,9\) (nghìn đồng)
Số tiền phải trả tương ứng với lượng điện 100kWh là:
\(50.1,678 + (100 - 50).1,734 = 170,6\)(nghìn đồng)
Số tiền phải trả tương ứng với lượng điện 200kWh là:
\(50.1,678 + (100 - 50).1,734 + (200 - 100).2,014 = 372\)(nghìn đồng)
Điền vào bảng ta có:
b) Công thức mô tả sự phụ thuộc y vào x khi\(0 \le x \le 50\) là:
\(y = 1,678.x\)

ĐKXĐ: ...
Đặt \(\left\{{}\begin{matrix}\sqrt[4]{56-x}=a\ge0\\\sqrt[4]{x^2+41}=b\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=5\\a^4+b^4=97\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\\left(a^2+b^2\right)^2-2a^2b^2=97\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\\left[\left(a+b\right)^2-2ab\right]^2-2a^2b^2=97\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\\left(25-2ab\right)^2-2a^2b^2=97\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\2a^2b^2-100ab+528=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\\left[{}\begin{matrix}ab=44\\ab=6\end{matrix}\right.\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}a+b=5\\ab=44\end{matrix}\right.\) (vô nghiệm)
TH2: \(\left\{{}\begin{matrix}a+b=5\\ab=6\end{matrix}\right.\) theo Viet đảo a;b là nghiệm:
\(t^2-5t+6=0\Rightarrow...\)

a) Thay x=100 ta được:
\(y = - {200.100^2} + 92000.100 - 8400000\)
\( = - 1200000\)
Thay x=200 ta được:
\(\begin{array}{l}y = - {200.200^2} + 92000.200 - 8400000\\ = 2000000\end{array}\)
Vậy với \(x = 100\) thì \(y = - 1200000\)
Với \(x = 200\) thì \(y = 2000000\)
b) Với mỗi giá trị của x có 1 giá trị tương ứng của y.

Xét dấu tam thức bậc hai tức là kiểm tra về dấu của tam thức bậc hai theo từng (khoảng) giá trị của ẩn.
Ta có \(a = - 200 < 0,b = 92 000, c = 8400 000\)
\(\Delta ' = {(92000:2)}^2 - \left( { - 200} \right). 8400 000 = 436000000 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = 230 \pm 10\sqrt 109\). Khi đó:
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( { - \infty ; 230 - 10\sqrt 109} \right)\) và \(\left( {230 + 10\sqrt 109; + \infty } \right)\);
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( {230-10\sqrt 109; 230 + 10\sqrt 109} \right)\)

Bài 1:
a)\(\begin{cases}\left(x-3\right)^2+\left(y+2\right)^2=0\\\begin{cases}\left(x-3\right)^2\ge0\\\left(y+2\right)^2\ge0\end{cases}\end{cases}\)
\(\Rightarrow\begin{cases}\left(x-3\right)^2=0\\\left(y+2\right)^2=0\end{cases}\)\(\Rightarrow\begin{cases}x=3\\y=-2\end{cases}\)
b) tương tự
b) (x-12+y)200+(x-4-y)200= 0
\(\begin{cases}\left(x-12+y\right)^{200}+\left(x-4-y\right)^{200}=0\\\begin{cases}\left(x-12+y\right)^{200}\ge0\\\left(x-4-y\right)^{200}\ge0\end{cases}\end{cases}\)
\(\Rightarrow\begin{cases}\left(x-12+y\right)^{200}=0\\\left(x-4-y\right)^{200}=0\end{cases}\)\(\Rightarrow\begin{cases}x-12+y=0\\x-4-y=0\end{cases}\)\(\Rightarrow\begin{cases}x+y=12\left(1\right)\\x-y=4\left(2\right)\end{cases}\)
Trừ theo vế của (1) và (2) ta được:
\(2y=8\Rightarrow y=4\)\(\Rightarrow\begin{cases}x+4=12\\x-4=4\end{cases}\)\(\Rightarrow x=8\)
Vậy x=8; y=4

1)
a) \(89-\left(73-x\right)=20\)
\(\Leftrightarrow73-x=89-20\)
\(\Leftrightarrow73-x=69\)
\(\Leftrightarrow x=73-69\)
\(\Leftrightarrow x=4\)
Vậy \(x=4\)
b) \(\left(x+7\right)-25=13\)
\(\Leftrightarrow x+7=13+25\)
\(\Leftrightarrow x+7=38\)
\(\Leftrightarrow x=38-7\)
\(\Leftrightarrow x=31\)
Vậy \(x=31\)
c) \(140:\left(x-8\right)=7\)
\(\Leftrightarrow x-8=140:7\)
\(\Leftrightarrow x-8=20\)
\(\Leftrightarrow x=20+8\)
\(\Leftrightarrow x=28\)
Vậy \(x=28\)
d) \(6x+x=5^{11}:5^9+3^1\)
\(\Leftrightarrow7x=5^{11}:5^9+3^1\)
\(\Leftrightarrow7x=5^{11-9}+3^1\)
\(\Leftrightarrow7x=5^2+3^1\)
\(\Leftrightarrow7x=25+3\)
\(\Leftrightarrow7x=28\)
\(\Leftrightarrow x=28:7\)
\(\Leftrightarrow x=4\)
Vậy \(x=4\)
e) \(4^x=64\)
\(\Leftrightarrow4^x=4^3\)
\(\Leftrightarrow x=3\)
Vậy \(x=3\)
g) \(9^{x-1}=9\)
\(\Leftrightarrow9^{x-1}=9^1\)
\(\Leftrightarrow x-1=1\)
\(\Leftrightarrow x=1+1\)
\(\Leftrightarrow x=2\)
Vậy \(x=2\)
\(4\left(x+41\right)-200=400\)
\(4\left(x+41\right)=400+200\)
\(4\left(x+41\right)=600\)
\(x+41=600:4\)
\(x+41=150\)
\(x=150-41\)
\(x=109\left(TM\right)\)
Vậy \(x=109\)