K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2021
1. Đề bài sai, các biểu thức này chỉ có giá trị lớn nhất, không có giá trị nhỏ nhất
2.
\(A=\left(2x\right)^3-3^3-\left(8x^3+2\right)\)
\(=8x^3-27-8x^3-2\)
\(=-29\)
\(B=x^3+9x^2+27x+27-\left(x^3+9x^2+27x+243\right)\)
\(=27-243=-216\)
26 tháng 7 2021
sửa đề lại thành tìm Max nhé1, vì mấy ý này ko có min
\(1,=>D=-\left(x^2-4x-3\right)=-\left(x^2-2.2x+4-7\right)\)
\(=-[\left(x-2\right)^2-7]=-\left(x-2\right)^2+7\le7\)
dấu"=" xảy ra<=>x=2
2, \(E=-2\left(x^2-x+\dfrac{5}{2}\right)=-2[x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{9}{4}]\)
\(=-2[\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}]\le-\dfrac{9}{2}\) dấu"=" xảy ra<=>x=1/2
3, \(F=-\left(x^2+4x-20\right)=-\left(x^2+2.2x+4-24\right)\)
\(=-[\left(x+2\right)^2-24]\le24\) dấu"=" xảy ra<=>x=-2
28 tháng 10 2021
\(a,=6x^3y-9xy^2z+3x^4y\\ c,=\left(2x+3-2x+3\right)^2+xy=81+xy\\ d,=\left(2x+1\right)^2:\left(2x+1\right)=2x+1\)
TT
3
9 tháng 9 2021
\(1,\\ a,A=4x^2\left(-3x^2+1\right)+6x^2\left(2x^2-1\right)+x^2\\ A=-12x^4+4x^2+12x^2-6x^2+x^2=-x^2=-\left(-1\right)^2=-1\\ b,B=x^2\left(-2y^3-2y^2+1\right)-2y^2\left(x^2y+x^2\right)\\ B=-2x^2y^3-2x^2y^2+x^2-2x^2y^3-2x^2y^2\\ B=-4x^2y^3-4x^2y^2+x^2\\ B=-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^3-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^2+\left(0,5\right)^2\\ B=\dfrac{1}{8}-\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{8}\)
9 tháng 9 2021
\(2,\\ a,\Leftrightarrow10x-16-12x+15=12x-16+11\\ \Leftrightarrow-14x=-4\\ \Leftrightarrow x=\dfrac{2}{7}\\ b,\Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\\ \Leftrightarrow-x^3=8=-2^3\\ \Leftrightarrow x=2\\ c,\Leftrightarrow4x^2\left(4x-2\right)-x^3+8x^2=15\\ \Leftrightarrow16x^3-8x^2-x^3+8x^2=15\\ \Leftrightarrow15x^3=15\\ \Leftrightarrow x^3=1\Leftrightarrow x=1\)
CM
31 tháng 3 2019
a) (2x – 1)(4x2 + 2x + 1) – 4x(2x2 – 3) = 23
⇔ 8x3 – 1 – 8x3 + 12x = 23
⇔ 12x = 24 ⇔ x = 2.
Tập nghiệm của phương trình: S = {2}
b) ĐKXĐ : x + 1 ≠ 0 và x – 2 ≠ 0 (vì vậy x2 – x – 2 = (x + 1)(x – 2) ≠ 0)
⇔ x ≠ -1 và x ≠ 2
Quy đồng mẫu thức hai vế :
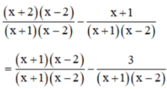
Khử mẫu, ta được : x2 – 4 – x – 1 = x2 – x – 2 – 3 ⇔ 0x = 0
Phương trình này luôn nghiệm đúng với mọi x ≠ -1 và x ≠ 2.
12 tháng 9 2021
a) \(A=x^2+3x+4=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
\(minA=\dfrac{7}{4}\Leftrightarrow x=-\dfrac{3}{2}\)
b) \(B=2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)
\(minB=\dfrac{7}{8}\Leftrightarrow x=\dfrac{1}{4}\)
c) \(C=5x^2+2x-3=5\left(x+\dfrac{1}{5}\right)^2-\dfrac{16}{5}\ge-\dfrac{16}{5}\)
\(minC=-\dfrac{16}{5}\Leftrightarrow x=-\dfrac{1}{5}\)
d) \(D=4x^2+4x-24=\left(2x+1\right)^2-25\ge-25\)
\(minD=-25\Leftrightarrow x=-\dfrac{1}{2}\)
e) \(E=x^2+6x-11=\left(x+3\right)^2-20\ge-20\)
\(minE=-20\Leftrightarrow x=-3\)
f) \(G=\dfrac{1}{4}x^2+x-\dfrac{1}{3}=\left(\dfrac{1}{2}x+1\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\)
\(minG=-\dfrac{4}{3}\Leftrightarrow x=-2\)
12 tháng 9 2021
\(A=x^2+3x+4=\left(x^2+3x+\dfrac{9}{4}\right)+\dfrac{7}{4}=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\)
Do \(\left(x+\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
\(minA=\dfrac{7}{4}\Leftrightarrow x+\dfrac{3}{2}=0\Leftrightarrow x=-\dfrac{3}{2}\)
Mấy câu còn lại làm tương tự nhé em^^
26 tháng 11 2022
a: ĐKXĐ của A là x<>1; x<>-3
ĐKXĐ của B là x<>4
ĐKXĐ của C là x<>0; x<>2
ĐKXĐ của D là x<>3
ĐKXĐ của E là x<>0; x<>2
b: \(A=\dfrac{2x\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}=\dfrac{2x}{x-1}\)
Để A=0 thì 2x=0
=>x=0
\(B=\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x-4\right)^2}=\dfrac{x+4}{x-4}\)
Để B=0 thì x+4=0
=>x=-4
\(C=\dfrac{x\left(x+2\right)}{x\left(x-2\right)}=\dfrac{x+2}{x-2}\)
Để C=0 thì x+2=0
=>x=-2
\(D=\dfrac{\left(x+4\right)\left(x-3\right)}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x+4}{x^2+3x+9}\)
Để D=0 thi x+4=0
=>x=-4
\(E=\dfrac{2x\left(x^2+2x+1\right)}{2x\left(x-2\right)}=\dfrac{\left(x+1\right)^2}{x-2}\)
Để E=0 thì (x+1)^2=0
=>x=-1
5 tháng 10 2021
\(A=\left(2x-1\right)^2+9\ge9\\ A_{min}=9\Leftrightarrow x=\dfrac{1}{2}\\ B=2\left(x^2-2\cdot\dfrac{3}{4}x+\dfrac{9}{16}\right)+\dfrac{1}{8}=2\left(x-\dfrac{3}{4}\right)^2+\dfrac{1}{8}\ge\dfrac{1}{8}\\ B_{min}=\dfrac{1}{8}\Leftrightarrow x=\dfrac{3}{4}\\ C=\left(4x^2+4xy+y^2\right)+2\left(2x+y\right)+1+\left(y^2+4y+4\right)-4\\ C=\left[\left(2x+y\right)^2+2\left(2x+y\right)+1\right]+\left(y+2\right)^2-4\\ C=\left(2x+y+1\right)^2+\left(y+2\right)^2-4\ge-4\\ C_{min}=-4\Leftrightarrow\left\{{}\begin{matrix}2x=-1-y\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=-2\end{matrix}\right.\)
\(D=\left(3x-1-2x\right)^2=\left(x-1\right)^2\ge0\\ D_{min}=0\Leftrightarrow x=1\\ G=\left(9x^2+6xy+y^2\right)+\left(y^2+4y+4\right)+1\\ G=\left(3x+y\right)^2+\left(y+2\right)^2+1\ge1\\ G_{min}=1\Leftrightarrow\left\{{}\begin{matrix}3x=-y\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-2\end{matrix}\right.\)
5 tháng 10 2021
\(H=\left(x^2-2xy+y^2\right)+\left(x^2+2x+1\right)+\left(2y^2+4y+2\right)+2\\ H=\left(x-y\right)^2+\left(x+1\right)^2+2\left(y+1\right)^2+2\ge2\\ H_{min}=2\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=-1\\y=-1\end{matrix}\right.\Leftrightarrow x=y=-1\)
Ta luôn có \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2yz-2xz\ge0\\ \Leftrightarrow x^2+y^2+z^2\ge xy+yz+xz\\ \Leftrightarrow x^2+y^2+z^2+2xy+2yz+2xz\ge3xy+3yz+3xz\\ \Leftrightarrow\left(x+y+z\right)^2\ge3\left(xy+yz+xz\right)\\ \Leftrightarrow\dfrac{3^2}{3}\ge xy+yz+xz\\ \Leftrightarrow K\le3\\ K_{max}=3\Leftrightarrow x=y=z=1\)
\(4x\left(2x^2-1\right)+27=\left(4x^2+6x\right)\left(2x+3\right)\)
<=> \(2x\left[2\left(2x^2-1\right)\right]=2x\left(2x+3\right)\left(2x+3\right)\)
<=> \(2x\left(4x^2-2\right)=2x\left(2x+3\right)^2\)
<=> \(2x\left(4x^2-2\right)-2x\left(2x+3\right)^2=0\)
<=> \(2x\left(4x^2-2\right)-2x\left(4x^2+12x+6\right)=0\)
<=> \(2x\left(4x^2-2-4x^2+12x+6\right)=0\)
<=> \(2x\left(12x-4\right)=0\)
<=> \(\orbr{\begin{cases}x=0\\12x-4=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=0\\x=\frac{1}{3}\end{cases}}\)