
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Từ pt dưới:
\(x^2+9y^2=6xy\Leftrightarrow x^2-6xy+9y^2=0\)
\(\Leftrightarrow\left(x-3y\right)^2=0\Leftrightarrow x-3y=0\Leftrightarrow x=3y\)
Thế lên pt trên: \(2.\left(3y\right)^2+y^2=19\)
\(\Leftrightarrow19y^2=19\Leftrightarrow y^2=1\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=3\\y=-1\Rightarrow x=-3\end{matrix}\right.\)

\(\hept{\begin{cases}3x^2+6xy-x+3y=0\\4x-9y=6\left(1\right)\end{cases}}\)
+, \(x=0\)thì hpt đã cho vô nghiệm
+, \(x\ne0\), nhân cả 2 vế của (1) với x ,ta được hpt:
\(\hept{\begin{cases}3x^2+6xy-x+3y=0\left(2\right)\\4x^2-9xy-6x=0\left(3\right)\end{cases}}\)
Cộng (2) và (3),vế với vế ta được
\(7x^2-3xy-7x+3y=0\)
\(\Leftrightarrow x\left(7x-3y\right)-\left(7x-3y\right)=0\)
\(\Leftrightarrow\left(7x-3y\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\7x-3y=0\end{cases}}\)
+,\(x-1=0\Rightarrow x=1\Rightarrow y=-\frac{2}{9}\)
+,\(7x-3y=0\Rightarrow x=\frac{3y}{7}\),thay vào (1),ta được
\(4\cdot\frac{3y}{7}-9y=6\)\(-51y=42\Rightarrow y=-\frac{13}{17}\Rightarrow x=-\frac{6}{17}\)
Vậy....
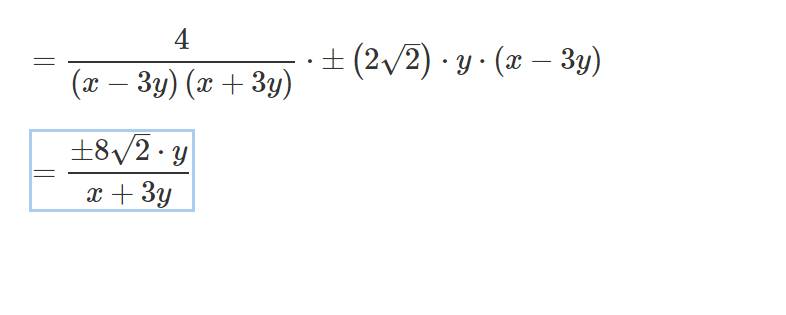
\(=\dfrac{4}{\left(x-3y\right)\left(x+3y\right)}\cdot\pm\left(2\sqrt{2}\right)\cdot y\cdot\left(x-3y\right)\)
\(=\dfrac{\pm8\sqrt{2}\cdot y}{x+3y}\)