Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì L và M đối xứng qua đường thẳng xy. Nên đường thẳng xy là trung trực của ML
I ∈ xt => IM = IL
Nên IM + IN = IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không là giao điểm của NL và xy thì ba điểm I, N, L không thẳng hàng
=> IL + IN > LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN
Vì L và M đối xứng qua đường thẳng xy. Nên đường thẳng xy là trung trực của ML
I ∈ xt => IM = IL
Nên IM + IN = IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không là giao điểm của NL và xy thì ba điểm I, N, L không thẳng hàng
=> IL + IN > LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN

Vì L và M đối xứng qua đường thẳng xy nên xy là đường thẳng đi qua trung điểm và vuông góc với ML.
Nên đường thẳng xy là trung trực của ML.
I ∈ xy ⇒ IM = IL (theo định lý 1).
Nên IM + IN = IL + IN
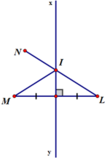
- TH1: Nếu I, L, N thẳng hàng
⇒ IL + IN = LN (vì N và L nằm khác phía so với đường thẳng xy và I nằm trên xy).
⇒ IM + IN = LN
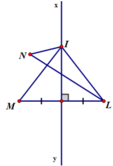
- TH2: Nếu I không là giao điểm của LN và xy thì ba điểm I, L, N không thẳng hàng
Áp dụng bất đẳng thức tam giác vào Δ INL ta được: IL + IN > LN
mà IM = IL (cmt)
⇒ IL + IN > LN (bất đẳng thức tam giác)
⇒ IM + IN > LN
Vậy với mọi vị trí của I trên xy thì IM + IN ≥ LN

ướng dẫn:
Vì L và M đối xứng qua đường thẳng xy. Nên đường thẳng xy là trung trực của ML
I ∈ xt => IM = IL

Nên IM + IN = IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không là giao điểm của NL và xy thì ba điểm I, N, L không thẳng hàng
=> IL + IN > LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN
48. Hai điểm M và N cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng xy.
Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN.
Hướng dẫn:
Vì L và M đối xứng qua đường thẳng xy. Nên đường thẳng xy là trung trực của ML
I ∈ xt => IM = IL

Nên IM + IN = IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không là giao điểm của NL và xy thì ba điểm I, N, L không thẳng hàng
=> IL + IN > LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN

L đối xứng với M qua xy
I thuộc xy
=> IM = IL
Xét \(\Delta ILN\)
IL + IN > LN ( BĐT tam giác)
Hay IM + IN > LN
#Hk_tốt
#Ngọc's_Ken'z

L đối xứng M qua xy
\(I\in xy\)
\(\Rightarrow IM=IL\)
Xét \(\Delta ILN\)
\(IL+IN>LN\left(Bđt\Delta\right)\)
Hay \(IM+IN>LN\)

Vì L và M đối xứng qua đường thẳng xy . Nên đường thẳng xy là trung trực của ML
I e xy => IM = IL
Nên IM + IL =IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không phải là giao điểm NL va xy thì ba điểm I , N, L không thẳng hàng
=> IL + IN = LN
Vậy với mọi vị trí của I trên xy thì IL + IN lớn hơn hoặc bằng LN
k mk nha kb luôn

Vì L và M đối xứng qua đường thẳng xy. Nên đường thẳng xy là trung trực của ML
I ∈ xt => IM = IL
Nên IM + IN = IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không là giao điểm của NL và xy thì ba điểm I, N, L không thẳng hàng
=> IL + IN > LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN