K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
0
NH
1
11 tháng 5 2017
Vì x=14 nên 15=x+1
\(A\left(x\right)=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}-...+\left(x+1\right)x^3-\left(x+1\right)x^2+\left(x+1\right)x-15\)
\(A\left(x\right)=x^{15}-x^{15}-x^{14}+x^{14}-x^{13}+...+x^4+x^3-x^3+x^2+x^2+x-15\)
\(A\left(x\right)=x^2+x^2+x-15\)
\(\Leftrightarrow A\left(x\right)=14^2+14^2+14-15=196+196-1\)
\(A\left(x\right)=391\)
11 tháng 11 2017
<=> 405 - 105x = 270 - 45x
<=> -105x + 45x = - 405 + 270
<=> -60x = -180
<=> x = 3
8 tháng 8 2022
\(3^{x+2}\cdot5^y=45^x\)
\(\Leftrightarrow3^{x+2}\cdot5^y=3^{2x}\cdot5^x\)
=>x=y và 2x=x+2
=>x=y=2
JT
1
20 tháng 4 2019
Ta thấy \(x=14\Rightarrow x+1=15\)
Thay x+1=15 vào biểu thức A ta được:
\(A=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}-...-\left(x+1\right)x^2+\left(x+1\right)x-1\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}-...-x^3-x^2+x^2+x-1\)
\(=x-1\)(1)
Thay x=14 vào (1) ta được :
\(A=14-1\)
\(=13\)
9 tháng 5 2017
Vì x=14 nên x+1=15
Thay 15=x+1 vào A(x) ta có:
A(x)= x15-(x+1)x14+(x+1)x13-(x+1)x12+...+(x+1)x3-(x+1)x2+(x+1)x-15
= x15-x15-x14+x14+x13-x13-x12+...+x4+x3-x3-x2+x2-x-15
= x-15
=> A(14) = 14-15=-1
Vậy A(14) = -1
9 tháng 5 2017
b.* Với x=0 ta có:
0.f(-4)=-2.f(0)
=> 0=-2.f(0) => f(0)=0
=> đa thức f(x) có 1 nghiệm là 0 (1)
* với x=2 ta có: 2.f(-2)=0.f(2)
=> 2.f(2)=0 => f(2)=0
=> 2 là nghiệm của đa thức f(x) (2)
Từ (1) và (2) => đa thức f(x) có ít nhất 2 nghiệm
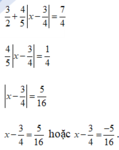
trình bày nhé ko ghi kết quả
\(45^x:15^x=81\)
\(\Leftrightarrow3^x=81\)
hay x=4