K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VD
13 tháng 3 2022
Ta có: \(\Delta=5^2-5.3.1=25-12=13>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=-1\end{matrix}\right.\)
\(K=\left(3x_1-1\right)\left(3x_2-1\right)+3\\ =3x_1x_2-3x_2-3x_1+1+3=3.\left(-1\right)-3\left(x_1+x_2\right)+4\\ =-3+4-3\left(-5\right)\\ =1+15\\ =16\)
CM
28 tháng 6 2017
Phương trình −3 x 2 + 5x + 1 = 0 có ∆ = 5 2 – 4.1.(−3) = 37 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = - 5 - 3 ⇔ x 1 + x 2 = 5 3
Đáp án: D
PT
Giải phương trình bằng cách đưa về phương trình tích:
3 x 2 - 7 x - 10 . 2 x 2 + 1 - 5 x + 5 - 3 = 0
1
CM
19 tháng 2 2018
(3x2 – 7x – 10).[2x2 + (1 – 5)x + 5 – 3] = 0
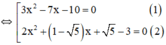
+ Giải (1):
3x2 – 7x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x1 = -1 và x2 = -c/a = 10/3.
QUẢNG CÁO+ Giải (2):
2x2 + (1 - √5)x + √5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
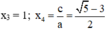
Vậy phương trình có tập nghiệm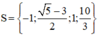 
CM
30 tháng 12 2018
a) 3 x 2 + 5x - 1 = 0
Ta có: a = 3; b = 5; c = -1
Δ = b 2 - 4ac = 5 2 - 4.3.(-1) = 37 > 0
Phương trình có 2 nghiệm phân biệt:
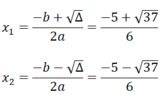
Vậy phương trình đã cho có tập nghiệm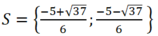 
CM
22 tháng 8 2019
(3x2 – 5x + 1)(x2 – 4) = 0
⇔ 3x2 – 5x + 1 = 0 (1)
hoặc x2 – 4 = 0 (2)
+ Giải (1): 3x2 – 5x + 1 = 0
Có a = 3; b = -5; c = 1 ⇒ Δ = (-5)2 – 4.3 = 13 > 0
Phương trình có hai nghiệm: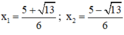 
+ Giải (2): x2 – 4 = 0 ⇔ x2 = 4 ⇔ x = 2 hoặc x = -2.
Vậy phương trình có tập nghiệm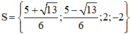 
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
\(\dfrac{x_1}{x_2-1}+\dfrac{x_2}{x_1-1}=\dfrac{x_1\left(x_1-1\right)+x_2\left(x_2-1\right)}{\left(x_1-1\right)\left(x_2-1\right)}\)
\(=\dfrac{x_1^2+x_2^2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{\left(-\dfrac{5}{3}\right)^2-2.\left(-2\right)-\left(-\dfrac{5}{3}\right)}{-2-\left(-\dfrac{5}{3}\right)+1}=...\)
CM
13 tháng 11 2019
Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
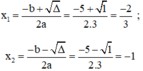
Vậy phương trình có hai nghiệm là -1 và 
PT
1
