Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=(1+2+2^2)+2^3(1+2+2^2)+...+2^96(1+2+2^2)+2^99
=7(1+2^3+...+2^96)+2^99 ko chia hết cho 7

a: \(G=8^8+2^{20}\)
\(=2^{24}+2^{20}\)
\(=2^{20}\left(2^4+1\right)=2^{20}\cdot17⋮17\)
b: Sửa đề: \(H=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\left(1+2\right)\)
\(=3\left(2+2^3+...+2^{59}\right)⋮3\)
\(H=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\left(2+2^4+...+2^{58}\right)⋮7\)
\(H=2+2^2+2^3+...+2^{60}\)
\(=\left(2+2^2+2^3+2^4\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2\left(1+2+2^2+2^3\right)+...+2^{57}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+...+2^{57}\right)⋮15\)
c: \(E=\left(1+3+3^2\right)+3^3\left(1+3+3^2\right)+...+3^{1989}\left(1+3+3^2\right)\)
\(=13\left(1+3^3+...+3^{1989}\right)⋮13\)
\(E=1+3+3^2+3^3+...+3^{1991}\)
\(=\left(1+3+3^2+3^3+3^4+3^5\right)+\left(3^6+3^7+3^8+3^9+3^{10}+3^{11}\right)+...+3^{1986}+3^{1987}+3^{1988}+3^{1989}+3^{1990}+3^{1991}\)
\(=364\left(1+3^6+...+3^{1986}\right)⋮14\)

\(B=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+...+2^{58}\right)⋮7\)


Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích sao cho tổng đó thành tích các thừa số trong đó có một thừa số chia hết cho 7. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: A = 2 + 2 2 + 2 3 + … + 2 60 = 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + … + 2 58 + 2 59 + 2 60 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2 + 2 4 + … + 2 58 .7 ⇒ A ⋮ 7 |

1. \(S=\left(1-\frac{1}{2^2}\right).\left(1-\frac{1}{3^2}\right)...\left(1-\frac{1}{100^2}\right)\)
\(S=\left(1-\frac{1}{4}\right).\left(1-\frac{1}{9}\right)...\left(1-\frac{1}{10000}\right)\)
\(S=\frac{3}{4}.\frac{8}{9}...\frac{9999}{10000}\)
\(S=\frac{1.3}{2.2}.\frac{2.4}{3.3}...\frac{99.101}{100.100}\)
\(S=\frac{1.2...99}{2.3...100}.\frac{3.4...101}{2.3...100}\)
\(S=\frac{1}{100}.\frac{101}{2}\)
\(S=\frac{101}{200}\)
2.
Vì 3x - 5y \(⋮\)23
\(\Rightarrow\)6 . ( 3x - 5y ) \(⋮\)23
Ta có : 6 . ( 3x - 5y ) + ( 5x - 16y )
\(\Leftrightarrow\)( 18x - 30y ) + ( 5x - 16y )
\(\Leftrightarrow\)23x - 46y
\(\Leftrightarrow\)23 . ( x - 2y ) \(⋮\)23
Vì 18x - 30y \(⋮\)23 mà ( 5 ; 23 ) = 1
\(\Rightarrow\)5x - 16y \(⋮\)23

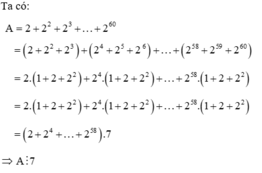
\(3^{x-1}.7+3^{x-1}.2=9\\ 3^{x-1}.\left(7+2\right)=9\\ 3^{x-1}.9=9\\ 3^{x-1}=\dfrac{9}{9}=1\\ Mà:3^0=1\\ Nên:x-1=0\\ Vậy:x=0+1=1\\ ---\\ P=2+2^2+2^3+...+2^{65}+2^{66}=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{64}+2^{65}+2^{66}\right)\\ =2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{64}\left(1+2+2^2\right)\\ =2.7+2^4.7+...+2^{64}.7\\ =\left(2+2^4+....+2^{64}\right).7⋮7\left(đpcm\right)\)
+)
\(3^{x-1}.7+3^{x-1}.2=9\)
\(3^{x-1}.\left(7+2\right)=9\)
\(3^{x-1}.9=9\)
\(3^{x-1}=9:9\)
\(3^{x-1}=1\)
⇔\(3^{x-1}=3^0\)
⇒\(x-1=0\)
\(x=0+1\)
\(x=1\)
Vậy \(x=1\)
+)
\(2+2^2+2^3+...+2^{65}+2^{66}\)
Vì \(2+2^2+2^3=14\) mà \(14\)⋮\(7\)
⇒Ta nhóm 3 số với nhau
Ta có:
\(\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{64}+2^{65}+2^{66}\right)\)
\(\left(2+2^2+2^3\right)+2^3.\left(2+2^2+2^3\right)+...+2^{63}.\left(2+2^2+2^3\right)\)
\(14.1+14.2^3+...+14.2^{63}\)
\(14.\left(1+2^3+...+2^{63}\right)\)
Do \(14\)⋮\(7\) nên \(P=14.\left(2+2^3+...+2^{63}\right)\)⋮\(7\)
Xin tick