
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TL ;
12:{400:[500-(125+25.7)]}
= 12 : { 400 : [ 500 - ( 125 + 175 )]}
= 12 : { 400 : 200 }
= 12 : 2
= 6
\(12\div\left\{400\div\left[500-\left(125+25.7\right)\right]\right\}\)
\(=\)\(12\div\left\{400\div\left[500-\left(125+175\right)\right]\right\}\)
\(=\)\(12\div\left\{400\div\left[500-300\right]\right\}\)
\(=\)\(12\div\left\{400\div200\right\}\)
\(=\)\(12\div2\)
\(=\)\(6\)

5x + 13 ⋮ 2x + 1
=> 5x + 2,5 + 11,5 ⋮ 2x + 1
=> 2,5(2x + 1) + 11,5 ⋮ 2x + 1
=> 11,5 ⋮ 2x + 1
=> 23 ⋮ 2x + 1
=> ...
=>5x+13chia hết cho 2x+1
ta có : 2(5x+13) chia hết 2x+1
5(2x+1) chia hết 2x+1
=>10x+26 chia hết 2x+1
10x +5 chia hết 2x+1
=>[(10x+26)-(10x+5)]chia hết 2x+1
=>21chia hết 2x+1 hay 2x +1 thược Ư(21) =(1 ;3;7;21;-1;-3;-7;-21)
ta có bảng:
| 2x+1 | 1 | 3 | 7 | -1 | -3 | -7 | 21 | -21 |
| x | 0 | 1 | 3 | -1 | -2 | -4 | 10 | -11 |
| nhận xét | chọn | chọn | chọn | chọn | chọn | chọn | chọn | chọn |
vậy x thuộc {0;1;3;-1;-2;-4;10;-11}

(x-3)^6=3.3.3.3.3.3=729
3.3.3.3.3.3.3=2187
vậy x của hai số là 729 và 2187.hai số trừ nhau bằng ko.


Trl :
2x + 5x + 7x = 22.7
14x = 4.7
14x = 28
x= 28 : 14
x = 2
Hok tốt
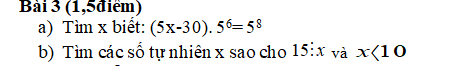
33
33