Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+ Khoảng cách giữa hai vật nhỏ trong quá trình dao động xác định theo công thức:
![]()
+ Đặt: X = x1 – x2 = 3cosωt - 6cos(ωt+π/3) = 3√3 sinωt
+ L có giá trị lớn nhất khi│X│ = Xmax = 3√3
=> Do vậy Lmax = 6cm.

Do 3 con lắc giống nhau, nên nó cùng vị trí cân bằng. 3 lò xo lại treo cách đều nhau, nên để 3 vật nhỏ gắn ở 3 lò xo luôn thẳng hàng thì con lắc ở giữa có li độ băng trung bình cộng của 2 con lắc kia (bạn có thể vẽ hình ra sẽ thấy rõ hơn)
\(\Rightarrow x_2=\frac{x_1+x_3}{2}\)
Tổng hợp 2 dao động x1 và x3 ta đc: \(x_1+x_3=24\cos\left(\pi t+\frac{5\pi}{12}\right)\)(cm)
\(\Rightarrow x_2=12\cos\left(\pi t+\frac{5\pi}{12}\right)\)

Đáp án B
Ta có: Khoảng cách giữa hai vật nhỏ của con lắc bằng: ![]()
Ta có:
![]()
Biên độ tổng hợp của
x
1
-
x
2
là:![]()
![]()
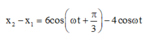
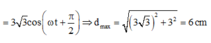

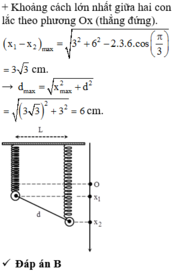






Do 3 con lắc giống hệt nhau nên nó có chung vị trí cân bằng. Ta có mối liên hệ li độ của 3 con lắc như sau:
Lấy D là trung điểm của AB. Ta có:
x1 + x2 = 2x2' (1)
x2' + x3 = 2x2 (2)
Rút x2' ở (2) thế vào (1):
x1 + x2 = 2(2x2 - x3)
Suy ra: \(x_3=\frac{1}{2}\left(3x_2-x_1\right)\)
Bạn lấy máy tính bấm biểu thức trên để tìm x3 nhé.
Bạn có thể tham khảo một bài tương tự ở đây nhé:
Hỏi đáp - Trao đổi kiến thức Toán - Vật Lý - Hóa Học - Sinh Học - Học và thi online với HOC24