Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

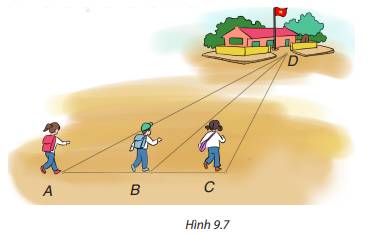
+ Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
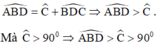
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.

Dễ mà, xem mình giải nè:
Trong tam giác BCD có:
góc ACD là góc tù=> BD là cạch lớn nhất của tam giác BCD ; hay BD>CD (1)
Vì góc ABD là góc ngoài của tam giác BCD=> góc ABD > góc ACD
Mà góc ACD là góc tù=> góc BCD là góc tù
Trong tam giác ABD có góc ABD là góc tù
=> AD là cạch lớn nhất của tam giác ABD
hay AD>BD (2)
Từ (1) và (2) => AD>BD>CD
Vậy Người đi xa nhất là Hạnh
Người đi gần nhất là Trang

Dễ mà, xem mình giải nè:
Trong tam giác BCD có:
góc ACD là góc tù=> BD là cạch lớn nhất của tam giác BCD ; hay BD>CD (1)
Vì góc ABD là góc ngoài của tam giác BCD=> góc ABD > góc ACD
Mà góc ACD là góc tù=> góc BCD là góc tù
Trong tam giác ABD có góc ABD là góc tù
=> AD là cạch lớn nhất của tam giác ABD
hay AD>BD (2)
Từ (1) và (2) => AD>BD>CD
Vậy Người đi xa nhất là Hạnh
Người đi gần nhất là Trang
Vì . = 900 nên ∆DCB có
=> BD > CD (1)
∆ABD có là góc ngoài của ∆DCB
=> >
nên là góc lớn nhất (vì
tù)
=> AD > BD (2)
Từ (1) và (2) => AD > BD >CD
Vậy Hạnh đi xa nhất, Trang đi gần nhất

Vì . = 900 nên ∆DCB có
=> BD > CD (1)
∆ABD có là góc ngoài của ∆DCB
=> >
nên là góc lớn nhất (vì tù)
=> AD > BD (2)
Từ (1) và (2) => AD > BD >CD
Vậy Hạnh đi xa nhất, Trang đi gần nhất

Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất. Do đó bạn Mai đi xa nhất, bạn Hà đi gần nhất.

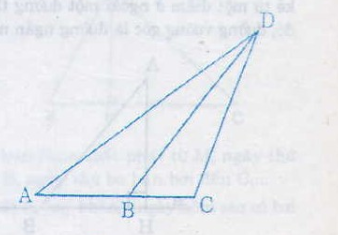
Ba bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường AD, BD, và CD (hình dưới). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng và góc ACD là góc tù. Hỏi ai đi xa nhất, ai đi gần nhất? Hãy giải thích
Hình 5
Lời giải:
Vậy bạn Hạnh đi xa nhất, bạn Trang đi gần nhất.
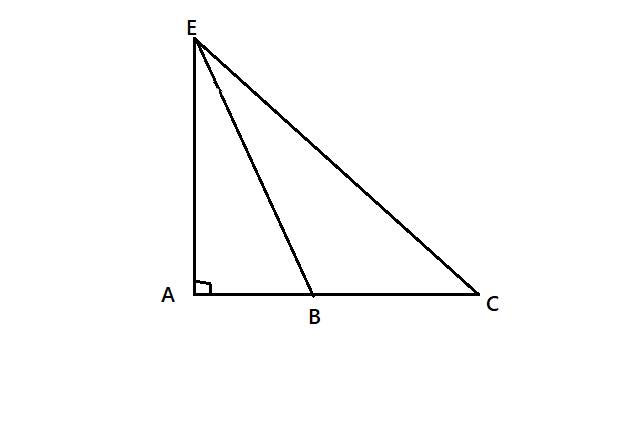 3 bạn AN , BÌNH , CHI đi đến trường theo con đường AE , BE , CE như hình trên . Biết rằng 3 điểm A , B , C cùng nằm trên 1 đường thẳng và góc EAC là góc vuông . Hỏi ai đi xa nhất , ai đi gần nhất . Giari thích ?
3 bạn AN , BÌNH , CHI đi đến trường theo con đường AE , BE , CE như hình trên . Biết rằng 3 điểm A , B , C cùng nằm trên 1 đường thẳng và góc EAC là góc vuông . Hỏi ai đi xa nhất , ai đi gần nhất . Giari thích ?

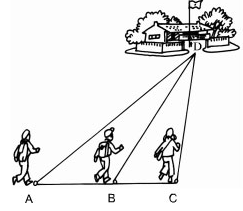

∆ABE có ∠A = 90⁰
⇒ ∠A lớn nhất
⇒ BE > AE (1)
∆CBE có
∠CBE là góc ngoài ∆ABE
⇒ ∠CBE = ∠A + ∠AEB
⇒ ∠CBE là góc tù
⇒ ∠CBE là góc lớn nhất của ∆CBE
⇒ CE > BE (2)
Từ (1) và (2) ⇒ CE > BE > AE
Vậy Chi đi xa nhất, An đi gần nhất