K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
9 tháng 7 2019
Không chắc đâu:v
a) Ta luôn có \(\left(x-1\right)^2+\left(2x-y-3\right)^2+\left(y+z\right)^2\ge0\forall x,y,z\)
Để đẳng thức xảy ra tức là \(\left(x-1\right)^2+\left(2x-y-3\right)^2+\left(y+z\right)^2=0\) (theo đề bài)
Thì \(\left\{{}\begin{matrix}x=1\\y=2x-3=2.1-3=-1\\z=-y=1\end{matrix}\right.\)
Vậy...
b) Ta luôn có \(VT\ge0\) với mọi x, y. Mà theo đề bài \(VT\le0\)
Do vậy \(VT=0\Leftrightarrow\left(2x+3\right)^{1998}+\left(3y-5\right)^{2000}=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-\frac{3}{2}\\y=\frac{5}{3}\end{matrix}\right.\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Các bất phương trình a), b), c) là các bất phương trình bậc nhất hai ẩn.
Bất phương trình d) không là bất phương trình bậc nhất hai ẩn vì có chứa \({y^2}.\)
24 tháng 9 2023
Tham khảo:
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
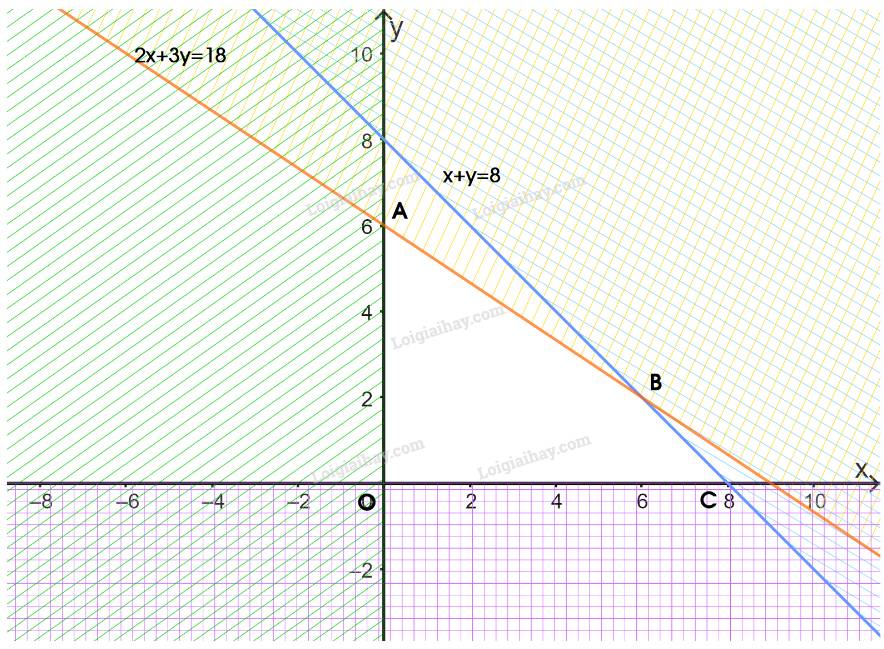
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Vẽ các đường thẳng \(2x - 3y = 6;2x + y = 2\) (nét đứt)
Thay tọa độ điểm O vào các bất phương trình trong hệ.
Ta thấy: 2.0-3.0
=> O thuộc miền nghiệm của cả 2 bất phương trình
Miền nghiệm:
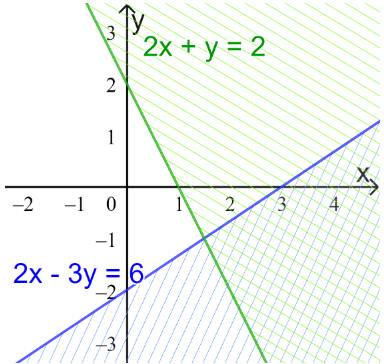
b)
Vẽ các đường thẳng
\(4x + 10y \le 20 \Leftrightarrow y = - \frac{2}{5}x + 2\) (nét liền)
\(x - y = 4 \Leftrightarrow y = x - 4\)(nét liền)
\(x = - 2\)(nét liền)
Thay tọa độ điểm O vào các bất phương trình trong hệ.
Ta thấy: 4.0+10.0-2
=> O thuộc miền nghiệm của cả 3 bất phương trình
Miền nghiệm:
c)
Vẽ các đường thẳng
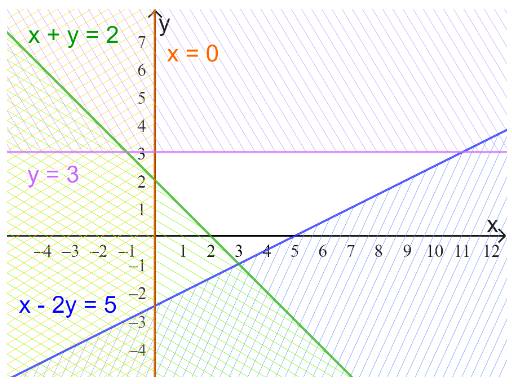
\(x - 2y = 5 \Leftrightarrow y = \frac{1}{2}x - 5\) (nét liền)
\(x + y = 2 \Leftrightarrow y = - x + 2\)(nét liền)
\(y = 3\)(nét liền)
Và trục Oy
Thay tọa độ O vào bất phương trình \(x - 2y \le 5\)
=> O thuộc miền nghiệm của bất phương trình trên.
Thay tọa độ O vào \(x + y \ge 2\)
=> O không thuộc miền nghiệm của bất phương trình trên
Lấy phần bên phải trục Oy và bên dưới đường thẳng y=3
Miền nghiệm:
D
1
T
24 tháng 7 2019
Áp dụng BĐT Bunhicopxki:
\(\left(\sqrt{\frac{1}{2}}^2+\sqrt{\frac{4}{3}}^2\right)\left(\left(\sqrt{2}x\right)^2+\left(\sqrt{3}y\right)^2\right)\ge\left(x+2y\right)^2\)
\(\Leftrightarrow\frac{11}{6}\left(2x^2+3y^2\right)\ge\left(x+2y\right)^2\)
\(\Leftrightarrow\frac{44}{6}=\frac{22}{3}\ge\left(x+2y\right)^2\)(1)
Do x, y > 0 nên x + 2y > 0 do đó từ (1) suy ra \(x+2y\le\sqrt{\frac{22}{3}}\)(đpcm)
ND
Nguyễn Đức Trí
VIP
6 tháng 10 2023
Bất phương trình bậc nhất 2 ẩn :
\(2x+3y>0\Rightarrow Câu\) \(C\)
\(x-2y\le1\Rightarrow Câu\) \(f\)
\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)
\(\Leftrightarrow4x-4+5y-15-2x+9>0\)
\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 10 2020
Do \(1\le x\le2\Rightarrow\left(x-1\right)\left(x-2\right)\le0\)
\(\Leftrightarrow x^2+2\le3x\)
Tương tự \(y^2+2\le3y\)
Do đó:
\(P=\frac{x+2y}{x^2+2+3y+3}+\frac{2x+y}{y^2+2+3x+3}+\frac{1}{4\left(x+y-1\right)}\ge\frac{x+2y}{3x+3y+3}+\frac{2x+y}{3x+3y+3}+\frac{1}{4\left(x+y-1\right)}\)
\(P\ge\frac{3x+3y}{3x+3y+3}+\frac{1}{4\left(x+y-1\right)}=\frac{x+y}{x+y+1}+\frac{1}{4\left(x+y-1\right)}\)
Đặt \(x+y=t\Rightarrow2\le t\le4\)
\(\Rightarrow P\ge\frac{t}{t+1}+\frac{1}{4t-4}=\frac{t}{t+1}+\frac{1}{4t-4}-\frac{7}{8}+\frac{7}{8}\)
\(P\ge\frac{\left(t-3\right)^2}{8\left(t^2-1\right)}+\frac{7}{8}\ge\frac{7}{8}\)
\(P_{min}=\frac{7}{8}\) khi \(t=3\) hay \(\left(x;y\right)=\left(1;2\right);\left(2;1\right)\)
Với mọi x, y ta có :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2000}\ge0\\\left(3y+4\right)^{2002}\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\ge0\)
Mà \(\left(2x-5\right)^{2000}+\left(3y+4\right)^{2002}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-5\right)^{2000}=0\\\left(3y+4\right)^{2002}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-5=0\\3y+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy..