K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
0
QM
0
ML
0
HT
23 tháng 2 2021
\(\int\dfrac{2x+1}{\left(x+1\right)^2+1}dx\)
\(x+1=\tan t\Rightarrow dx=\left(\tan^2t+1\right)dt\)
\(\Rightarrow\int\dfrac{2x+1}{\left(x+1\right)^2+1}dx=\int\dfrac{2\left(\tan t-1\right)+1}{\tan^2t+1}.\left(\tan^2t+1\right)dt\)
\(=\int(2\tan t-1)dt=\int2\tan t.dt-\int dt=2\int\tan t.dt-t\)
\(\int\tan t.dt=\int\dfrac{\sin t}{\cos t}.dt\)
\(u=\cos t\Rightarrow du=-\sin t.dt\Rightarrow\int\dfrac{\sin t}{\cos t}=-\int\dfrac{\sin t}{u}.\dfrac{du}{\sin t}=-ln \left|\cos t\right|+C\)
\(\Rightarrow\int\dfrac{2x+1}{x^2+2x+2}dx=-2ln\left|\cos t\right|-t=-2ln\left|\cos\left[arc\tan\left(x+1\right)\right]\right|-arc\tan\left(x+1\right)\)
P/s: Bạn tự thay cận vô nhé !
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2021
\(=\int\limits^1_0\dfrac{2x+2}{x^2+2x+2}dx-\int\limits^1_0\dfrac{1}{\left(x+1\right)^2+1}dx\)
\(=ln\left(x^2+2x+2\right)|^1_0-arctan\left(x+1\right)|^1_0=...\)
CM
11 tháng 3 2018
a) Bất phương trình đã cho tương đương với hệ sau:
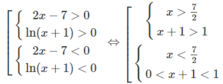
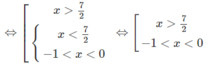
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
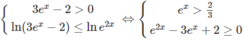
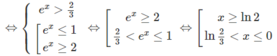
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 6 2019
a/ ĐKXĐ: \(x>\frac{1}{2}\)
\(\Leftrightarrow\frac{3x^2-1}{\sqrt{2x-1}}-\sqrt{2x-1}=mx\)
\(\Leftrightarrow\frac{3x^2-2x}{\sqrt{2x-1}}=mx\Leftrightarrow\frac{3x-2}{\sqrt{2x-1}}=m\)
Đặt \(\sqrt{2x-1}=a>0\Rightarrow x=\frac{a^2+1}{2}\Rightarrow\frac{3a^2-1}{2a}=m\)
Xét hàm \(f\left(a\right)=\frac{3a^2-1}{2a}\) với \(a>0\)
\(f'\left(a\right)=\frac{12a^2-2\left(3a^2-1\right)}{4a^2}=\frac{6a^2+2}{4a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến
Mặt khác \(\lim\limits_{a\rightarrow0^+}\frac{3a^2-1}{2a}=-\infty\); \(\lim\limits_{a\rightarrow+\infty}\frac{3a^2-1}{2a}=+\infty\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 6 2019
b/ ĐKXĐ: \(x\ge2\)
\(\Leftrightarrow\sqrt[4]{\left(x-1\right)^2}+4m\sqrt[4]{\left(x-1\right)\left(x-2\right)}+\left(m+3\right)\sqrt[4]{\left(x-2\right)^2}=0\)
Nhận thấy \(x=2\) không phải là nghiệm, chia 2 vế cho \(\sqrt[4]{\left(x-2\right)^2}\) ta được:
\(\sqrt[4]{\left(\frac{x-1}{x-2}\right)^2}+4m\sqrt[4]{\frac{x-1}{x-2}}+m+3=0\)
Đặt \(\sqrt[4]{\frac{x-1}{x-2}}=a\) pt trở thành: \(a^2+4m.a+m+3=0\) (1)
Xét \(f\left(x\right)=\frac{x-1}{x-2}\) khi \(x>0\)
\(f'\left(x\right)=\frac{-1}{\left(x-2\right)^2}< 0\Rightarrow f\left(x\right)\) nghịch biến
\(\lim\limits_{x\rightarrow2^+}\frac{x-1}{x-2}=+\infty\) ; \(\lim\limits_{x\rightarrow+\infty}\frac{x-1}{x-2}=1\) \(\Rightarrow f\left(x\right)>1\Rightarrow a>1\)
\(\left(1\right)\Leftrightarrow m\left(4a+1\right)=-a^2-3\Leftrightarrow m=\frac{-a^2-3}{4a+1}\)
Xét \(f\left(a\right)=\frac{-a^2-3}{4a+1}\) với \(a>1\)
\(f'\left(a\right)=\frac{-2a\left(4a+1\right)-4\left(-a^2-3\right)}{\left(4a+1\right)^2}=\frac{-4a^2-2a+12}{\left(4a+1\right)^2}=0\Rightarrow a=\frac{3}{2}\)
\(f\left(1\right)=-\frac{4}{5};f\left(\frac{3}{2}\right)=-\frac{3}{4};\) \(\lim\limits_{a\rightarrow+\infty}\frac{-a^2-3}{4a+1}=-\infty\)
\(\Rightarrow f\left(a\right)\le-\frac{3}{4}\Rightarrow m\le-\frac{3}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
a.
Pt giao điểm: \(cosx=0\Rightarrow x=\dfrac{\pi}{2}\)
\(S=\int\limits^{\pi}_0\left|cosx\right|dx=\int\limits^{\dfrac{\pi}{2}}_0cosxdx-\int\limits^{\pi}_{\dfrac{\pi}{2}}cosxdx=2\)
b.
Bạn coi lại đề, \(y=\dfrac{1}{2}x,x+\dfrac{1}{2}\) nghĩa là sao nhỉ?
c.
Pt giao điểm với Ox:
\(2-x-x^2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(S=\int\limits^1_{-2}\left(2-x-x^2\right)dx=\left(2x-\dfrac{1}{2}x^2-\dfrac{1}{3}x^3\right)|^1_{-2}=\dfrac{9}{2}\)
Lời giải:
Đặt \(2^{x^2}=a; 2^x=b\)
PT tương đương:
\(2.(2^{x^2})^2-9.2^{x^2}.2^x+4.(2^x)^2=0\)
\(\Leftrightarrow 2a^2-9ab+4b^2=0\)
\(\Leftrightarrow (a-4b)(2a-b)=0\)
TH1: \(a-4b=0\Leftrightarrow 2^{x^2}=4.2^x\Leftrightarrow 2^{x^2}=2^{x+2}\)
\(\Leftrightarrow x^2=x+2\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
TH2: \(2a-b=0\Leftrightarrow 2^{x^2+1}=2^x\Leftrightarrow x^2-x+1=0\)
\(\Leftrightarrow (x-\frac{1}{2})^2+\frac{3}{4}=0\) (vô lý)
Vậy \(x\in\left\{-1;2\right\}\)