2022x-2021 + 3 =( 7-5 )2 14* )( x+1) + ( x+2) +...+( x+30 ) = 795

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

NGUYỄN GIA QUÂN

20 tháng 10 2023

2022^x-2021+ 3 =( 7-5 )² 14^*)( x+1) + ( x+2) +...+( x+30 ) = 795

#Toán lớp 6

Nguyễn Lê Phước Thịnh

20 tháng 10 2023

Đúng(1)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NGUYỄN GIA QUÂN

19 tháng 10 2023

2022^x-2021+ 3 =( 7-5 )² 14^*( x+1) + ( x+2) +...+( x+30 ) = 795

#Toán lớp 6

Nguyễn Lê Phước Thịnh

20 tháng 10 2023

Đúng(0)

NGUYỄN GIA QUÂN

20 tháng 10 2023

2022x-2021 + 3 =( 7-5 )2 14* ( x+1) + ( x+2) +...+( x+30 ) =...

Đọc tiếp

#Toán lớp 6

Nguyễn Lê Phước Thịnh

20 tháng 10 2023

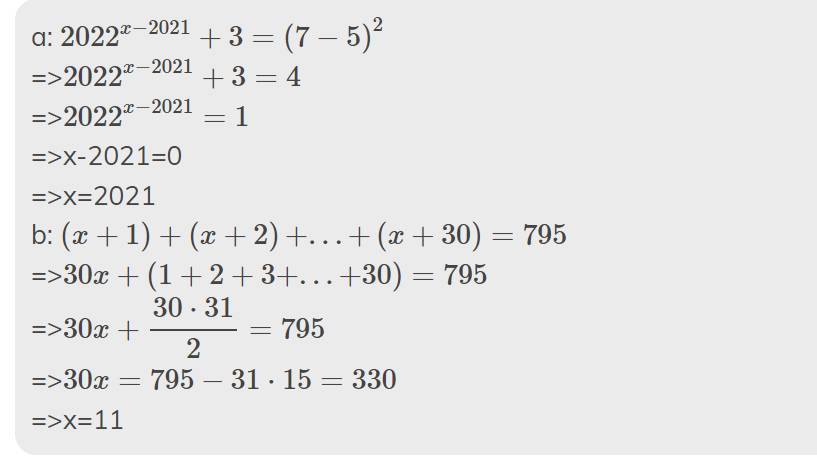
a: \(2022^{x-2021}+3=\left(7-5\right)^2\)

=>\(2022^{x-2021}+3=4\)

=>\(2022^{x-2021}=1\)

=>x-2021=0

=>x=2021

b: \(\left(x+1\right)+\left(x+2\right)+...+\left(x+30\right)=795\)

=>\(30x+\left(1+2+3+...+30\right)=795\)

=>\(30x+\dfrac{30\cdot31}{2}=795\)

=>\(30x=795-31\cdot15=330\)

=>x=11

Đúng(2)

Dang Truong Phat

13 tháng 10 2016 - olm

(x+1)+(x+2)+(x+3)+.....+(x+30)=795

#Toán lớp 6

13 tháng 10 2016

(x+1)+(x+2)+(x+3)+.....+(x+30)=795

(x+x+x+...+x)+(1+2+3+...+30)=795

30x+465=795

30x=795-465

30x=330

x=330:30

x=11

Đúng(0)

cong chua anna

13 tháng 10 2016

sai de

Đúng(0)

bùi lê vy

15 tháng 8 2015 - olm

Tim X : (x+1) + (x+2)+(x+3) +...+(x+30) =795

#Toán lớp 6

Nhok Silver Bullet

15 tháng 8 2015

(x+1) + (x+2)+(x+3) +...+(x+30) = 795

=> 30x + (1+2+3+...+29+30) = 795

=> 30x + 465 = 795 (1+2+3+...+30 bạn áp dụng quy tắc tính tổng dãy số cách đề là Ok)

=> 30x = 330

=> x = 11

Đúng(0)

vukhanhlinh

5 tháng 10 2017 - olm

1,Thực hiện phép tính hợp lý:2⁴¹+3⁸.(10⁷-2⁷).2⁴-4²

2,Tìm stn x biết rằng:x+1+x+2.(...+x+30)=795

#Toán lớp 6

Cao Xuan Linh

20 tháng 9 2016 - olm

a) 12:{390:[5.10 mu2-(5 mu3+7 mu2.x)]}=4

b) 3+2 mux-1=24-[4 mu2-(2 mu2-1)

c) (2x-6)mu2016=(2x-6)mu16

d) (x+1)+(x+2)+(x+3)+...+(x+30)=795

e) 2 mu x+2 mu x+4=272

Ai là người giải nhanh mình tick cho.Nhưng phải trả lời trước thứ 5 đấy nhé!

#Toán lớp 6

Bùi Xuân An

28 tháng 9 2023 - olm

Tìm số tự nhiên x biết:

(x+1)+(x+2)+(x+3)+...+(x+30)=795

Làm đúng cho TICK:)))

#Toán lớp 6

Trần Trang

28 tháng 9 2023

(x+1) + (x+2) + ... + (x+30) = 795

=> 30x + (1+2+... +30) = 795

=> 30x + 465 = 795

=> 30x = 330

=> x = 11

Đúng(0)

Rosé

5 tháng 10 2023

(x+1) + (x+2) + ......+ ( x+30) = 795

#Toán lớp 6

BÍCH THẢO

5 tháng 10 2023

(x+1)+(x+2)+...+(x+30)=795

(x+x+x+...+x) + (1+2+3+...+30) = 795

30x + 465 = 795

30x = 795 - 465

30x = 330

x = 330 : 30

x = 11

Vậy x = 11

tho T-T

Đúng(1)

Toru

5 tháng 10 2023

\((x+1)+(x+2)+...+(x+30)=795\\\Rightarrow (x+x+...+x)+(1+2+...+30)=795 (1)\)

Đặt \(A=1+2+...+30\)

Số các số hạng trong tổng \(A\) là:

\(\left(30-1\right):1+1=30\left(số\right)\)

Tổng \(A\) bằng:

\(\left(30+1\right)\cdot30:2=465\)

Thay \(A=465\) vào \(\left(1\right)\), ta được:

\(30x+465=795\\\Rightarrow 30x=795-465\\\Rightarrow 30x=330\\\Rightarrow x=330:30\\\Rightarrow x=11\)

#\(Toru\)

Đúng(1)

Nguyễn Bùi Anh Tuấn

28 tháng 9 2019 - olm

(x+1)+(x+2)+(x+3)+...+(x+29)+(x+30)=795

giai nhanh len,can gap

#Toán lớp 6

vũ việt nhật

28 tháng 9 2019

x.30+(1+2+3+......+29+30)=795

x.30+465=795

x.30=795-465

x.30=330

x=330:30

x=11

Đúng(0)

Nguyễn Minh Đức

28 tháng 9 2019

\(\text{(x+1)+(x+2)+(x+3)+...+(x+29)+(x+30)=795}\)

Số số hạng là:

(30-1):1+1 = 30 ( số hạng )

=> \(\text{x+1+x+2+x+3+...+x+29+x+30=795}\)

Đặt A = 1+2+3+...+30

A = \(\left(\left(30+1\right)\cdot30\right):2\)

A = 465

=> x+x+x+...+x+1+2+3+...+30=795

30x + 465 = 795

30x = 795 - 465 = 330

x = 330 : 30 = 11

Vậy x là 11

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP