
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2012+20122012+2013+20132013\)
\(=\left(2012+2013\right)+\left(20122012+20132013\right)\)
\(=4035+40354035\)
\(=40358070\)
Chúc bạn học tốt!!!

2013 x 20122012 - 2012 x 20132013
=2013 x 2012 x 10001 - 2012 x 2013 x 10001
=0
(mấy cái đậm-đậm; nghiêng-nghiêng; gạch chân-gạch chân là giản ước hết cho nhau nha!)


a) Ta có: \(\frac{2012}{2013}+\frac{1}{2013}=1\)
\(\frac{2013}{2014}+\frac{1}{2014}=1\)
Vì \(\frac{1}{2013}>\frac{1}{2014}\) nên \(\frac{2012}{2013}< \frac{2013}{2014}\)
Vậy: \(\frac{2012}{2013}< \frac{2013}{2014}\)
b) \(\frac{1006}{1007}+\frac{1}{1007}=1\)
\(\frac{2013}{2015}+\frac{2}{2015}=1\)
Mà \(\frac{1}{1007}=\frac{2}{2014}>\frac{2}{2015}\)
nên: \(\frac{1006}{1007}< \frac{2013}{2015}\)
Vậy:.......

Ta có : \(\frac{1}{2^2}< \frac{1}{1\cdot2}\)
\(\frac{1}{3^2}< \frac{1}{2\cdot3}\)
\(.\) \(.\)
\(.\)
\(.\) \(.\)
\(.\) \(.\)
\(\frac{1}{2013^2}< \frac{1}{2012\cdot2013}\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+.........+\frac{1}{2013^2}< \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+.....+\frac{1}{2012\cdot2013}\)
Mà \(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+.....+\frac{1}{2012\cdot2013}=1-\frac{1}{2013}< 1\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+......+\frac{1}{2013^2}< 1\)
Nhớ k cho mình nhé!
Chúc các bạn học tốt!
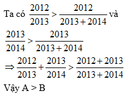
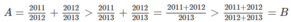
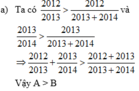
2013×20122012-2012×20132013
= (2013 . 20122012) - ( 2012 . 20132013)
= 40505610156 - 40505610156
= 0
2013×20122012-2012×20132013
= (2013 . 20122012) - ( 2012 . 20132013)
= 40505610156 - 40505610156
= 0