Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\frac{3x-2}{2}=\frac{1-2x}{3}\)
\(\Leftrightarrow3\left(3x-2\right)=2\left(1-2x\right)\)
\(\Leftrightarrow9x-6=2-4x\)
\(\Leftrightarrow13x-8=0\)
\(\Leftrightarrow x=\frac{8}{13}\)
b) \(\frac{x-1}{3}+2=3-\frac{2x+5}{4}\)
\(\Leftrightarrow\frac{4\left(x-1\right)+24}{12}=\frac{36-3\left(2x+5\right)}{12}\)
\(\Leftrightarrow4x-4+24=36-6x-15\)
\(\Leftrightarrow4x+20=-6x+21\)
\(\Leftrightarrow10x=1\)
\(\Leftrightarrow x=\frac{1}{10}\)
c) \(\frac{x-1}{5}+x=\frac{x+1}{7}\)
\(\Leftrightarrow\frac{7\left(x-1\right)+35x}{35}=\frac{5\left(x+1\right)}{7}\)
\(\Leftrightarrow7x-7+35x=5x+5\)
\(\Leftrightarrow37x=12\)
\(\Leftrightarrow x=\frac{12}{37}\)
d) \(2.\left(x-2.5\right)=0,25+\frac{4x-3}{8}\)
\(\Leftrightarrow8\left(x-2,5\right)=2+4x-3\)
\(\Leftrightarrow8x-20=4x-1\)
\(\Leftrightarrow4x=19\)
\(\Leftrightarrow x=\frac{4}{19}\)

a) 7x - 35 = 0
<=> 7x = 0 + 35
<=> 7x = 35
<=> x = 5
b) 4x - x - 18 = 0
<=> 3x - 18 = 0
<=> 3x = 0 + 18
<=> 3x = 18
<=> x = 5
c) x - 6 = 8 - x
<=> x - 6 + x = 8
<=> 2x - 6 = 8
<=> 2x = 8 + 6
<=> 2x = 14
<=> x = 7
d) 48 - 5x = 39 - 2x
<=> 48 - 5x + 2x = 39
<=> 48 - 3x = 39
<=> -3x = 39 - 48
<=> -3x = -9
<=> x = 3

Bài 1:
\(B=\frac{0,375-0,3+\frac{3}{11}+\frac{3}{12}}{-0,625+0,5-\frac{5}{11}-\frac{5}{12}}+\frac{1,5+1-0,75}{2,5+\frac{5}{3}-1,25}\)
\(=\frac{3\left(0,125-0,1+\frac{1}{11}+\frac{1}{12}\right)}{-\left(0,625-0,5+\frac{5}{11}+\frac{5}{12}\right)}+\frac{3\left(0,5+\frac{1}{3}-0,25\right)}{5\left(0,5+\frac{1}{3}-0,25\right)}\)
\(=\frac{3\left(0,125-0,1+\frac{1}{11}+\frac{1}{12}\right)}{-\left[5\left(0,125-0,1+\frac{1}{11}+\frac{1}{12}\right)\right]}+\frac{3}{5}\)
\(=\frac{-3}{5}+\frac{3}{5}\)
\(=0\)
Bài 2:
b) Giải:
Ta có: \(\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a^6}{b^6}=\frac{c^6}{d^6}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a^6}{b^6}=\frac{c^6}{d^6}=\frac{3a^6}{3b^6}=\frac{c^6}{d^6}=\frac{3a^6+c^6}{3b^6+d^6}\) (1)
\(\frac{a}{b}=\frac{c}{d}=\frac{a+b}{b+d}\)
\(\Rightarrow\left(\frac{a}{b}\right)^6=\left(\frac{a+c}{b+d}\right)^6=\frac{a^6}{b^6}=\frac{\left(a+c\right)^6}{\left(b+d\right)^6}\) (2)
Từ (1) và (2) \(\Rightarrow\frac{3a^6+c^6}{3b^6+d^6}=\frac{\left(a+c\right)^6}{\left(b+d\right)^6}\left(đpcm\right)\)

Sửa đề:
\(\frac{1}{a-b}+\frac{1}{a+b}+\frac{2a}{a^2+b^2}+\frac{4a^3}{a^4+b^4}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{a+b+a-b}{\left(a-b\right)\left(a+b\right)}+\frac{2a}{a^2+b^2}+\frac{4a^3}{a^4+b^4}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{2a}{a^2-b^2}+\frac{2a}{a^2+b^2}+\frac{4a^3}{a^4+b^4}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{2a\left(a^2-b^2+a^2+b^2\right)}{\left(a^2-b^2\right)\left(a^2+b^2\right)}+\frac{4a^3}{a^4+b^4}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{2a.2a^2}{\left(a^2-b^2\right)\left(a^2+b^2\right)}+\frac{4a^3}{a^4+b^4}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{4a^3}{a^4-b^4}+\frac{4a^3}{a^4+b^4}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{4a^3\left(a^4+b^4+a^4-b^4\right)}{a^4-b^4}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{4a^3.2a^4}{\left(a^4+b^4\right)\left(a^4-b^4\right)}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{8a^7}{a^8-b^8}+\frac{8a^7}{a^8+b^8}\)
\(=\frac{8a^7\left(a^8+b^8+a^8-b^8\right)}{\left(a^8-b^8\right)\left(a^8+b^8\right)}\)
\(=\frac{16a^{15}}{a^{16}-b^{16}}\)
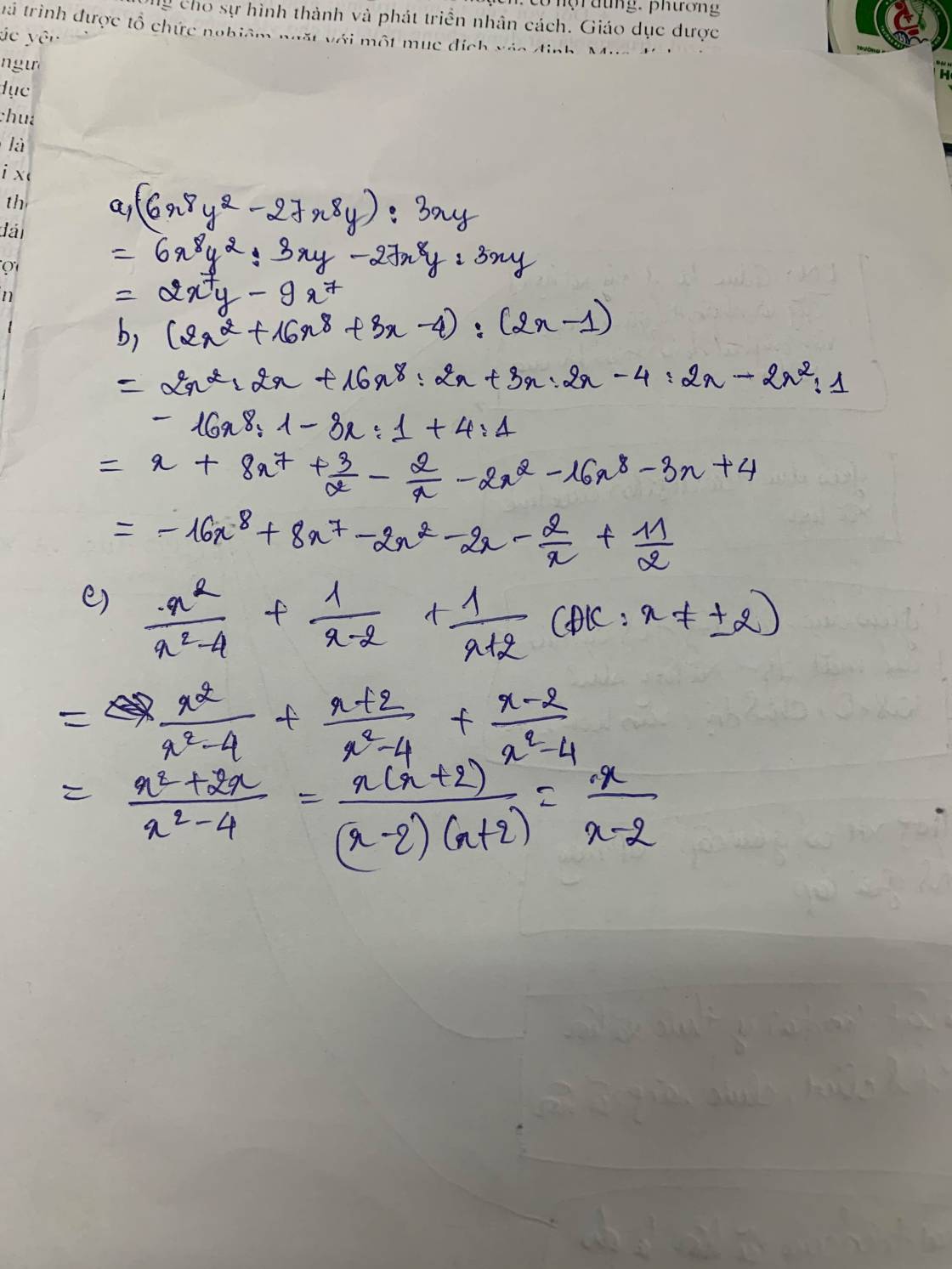
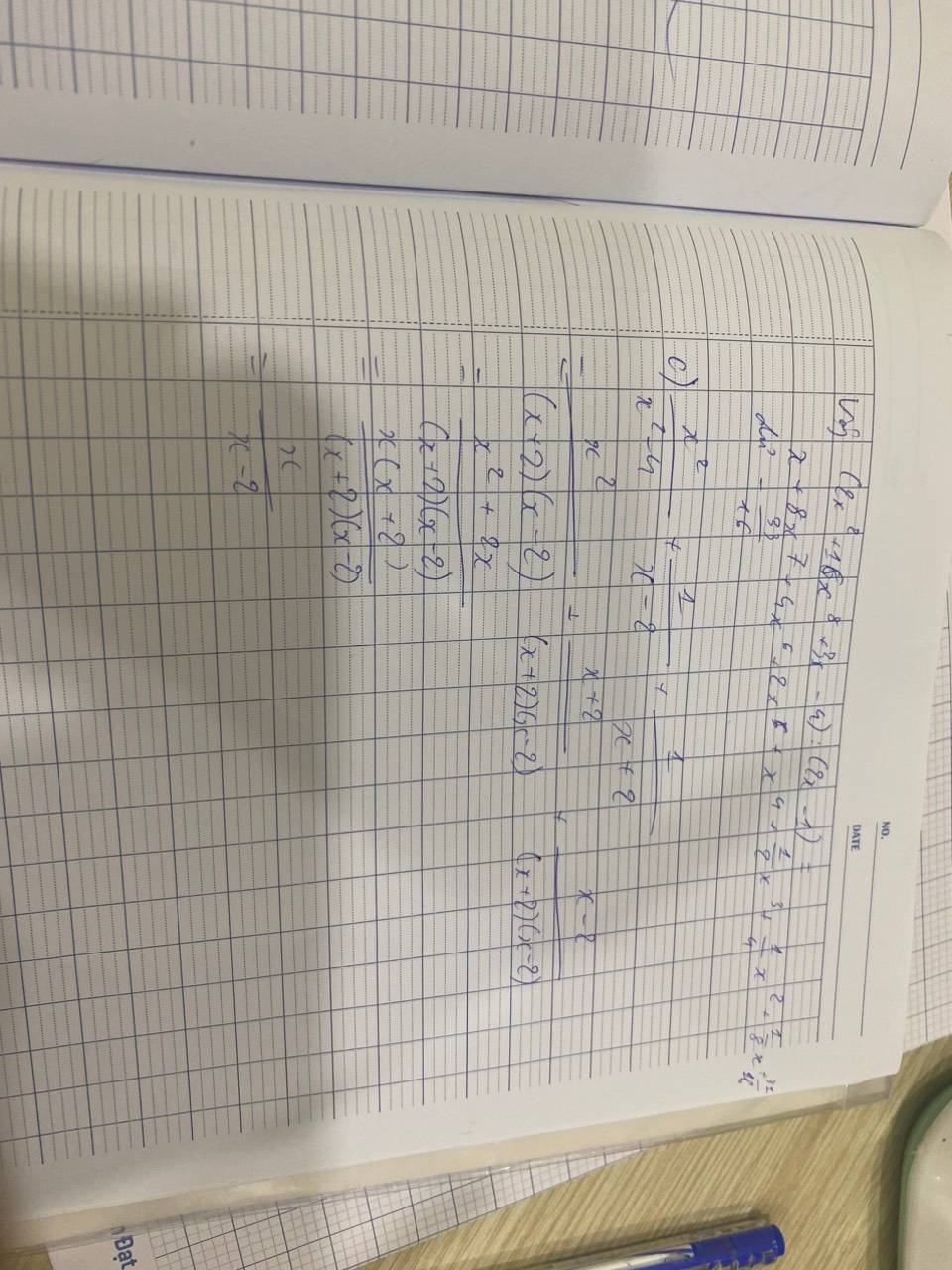
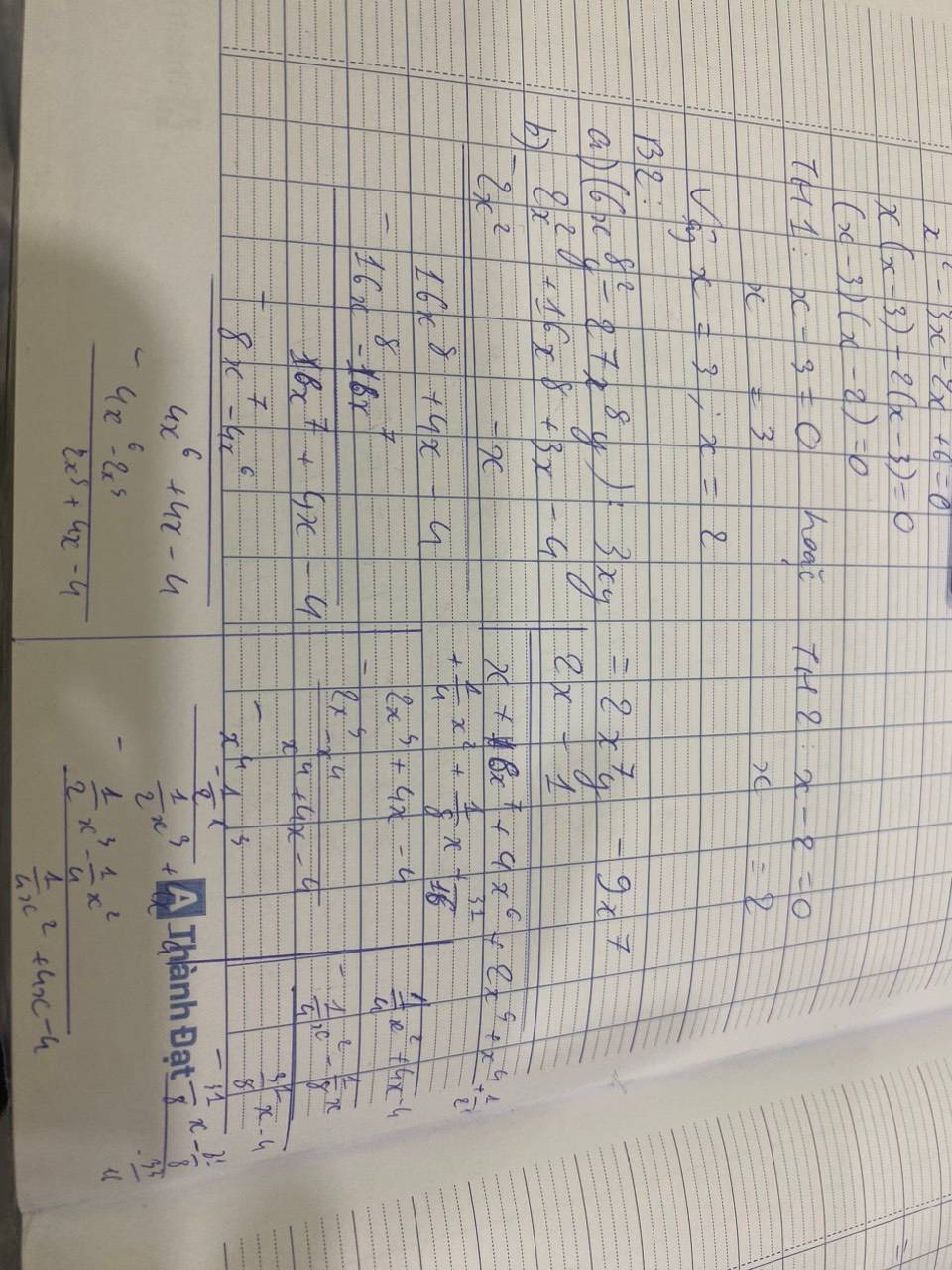
giải hộ mk nha mk đang cần gấp