Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tiết diện của dây thứ nhất: \(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p.l}{R}=\dfrac{1,7.10^{-8}1}{25}=6,8.10^{-10}m^2\)
Vì hai dây này làm cùng một chất liệu nên điện trở suất của chúng là như nhau.
Điện trở của dây thứ hai: \(R=p\dfrac{l}{S}=1,7.10^{-8}\dfrac{0,32}{6,8.10^{-10}}=8\Omega\)

Ta có:
\(R=\text{ρ}\dfrac{l}{S}\)
Do dây thứ nhất có chiều dài 20 cm và điện trở 8 ôm nên ta có:
\(8=\text{ρ}.\dfrac{\dfrac{20}{100}}{S}\Leftrightarrow\dfrac{\text{ρ}}{S}=40\)
Chiều dài dây thứ hai là:
\(l_2=\dfrac{R_2S}{\text{ρ }}=R_2.\dfrac{1}{40}\)
=> GT đề thiếu điện trở của dây thứ hai.

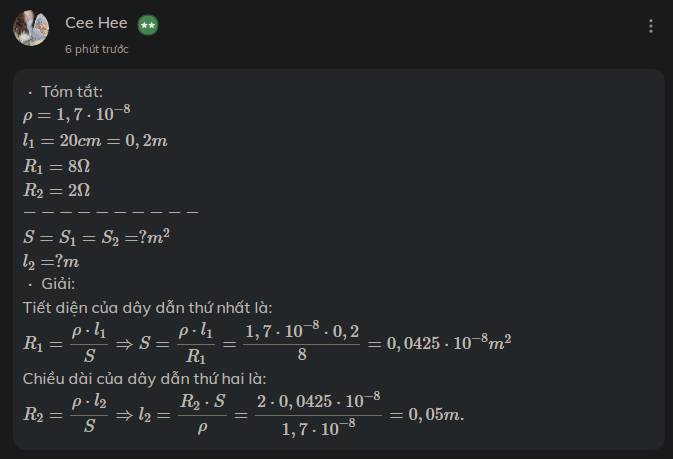
`*` Tóm tắt:
\(\rho=1,7\cdot10^{-8}\\ l_1=20cm=0,2m\\ R_1=8\Omega\\ R_2=2\Omega\\ ----------\\ S=S_1=S_2=?m^2\\ l_2=?m\)
`*` Giải:
Tiết diện của dây dẫn thứ nhất là:
\(R_1=\dfrac{\rho\cdot l_1}{S}\Rightarrow S=\dfrac{\rho\cdot l_1}{R_1}=\dfrac{1,7\cdot10^{-8}\cdot0,2}{8}=0,0425\cdot10^{-8}m^2\)
Chiều dài của dây dẫn thứ hai là:
\(R_2=\dfrac{\rho\cdot l_2}{S}\Rightarrow l_2=\dfrac{R_2\cdot S}{\rho}=\dfrac{2\cdot0,0425\cdot10^{-8}}{1,7\cdot10^{-8}}=0,05m.\)