Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lý phân giác cho tam giác ABM:
\(\dfrac{AM}{BM}=\dfrac{AD}{BD}\) (1)
Áp dụng định lý phân giác cho tam giác ACM:
\(\dfrac{AM}{CM}=\dfrac{AE}{CE}\) (2)
Mà AM là trung tuyến \(\Rightarrow BM=CM\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{CE}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+CE}\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\Rightarrow DE||BC\) (định lý talet đảo)

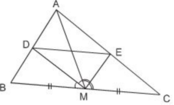
1: Xét ΔAMB có MD là phân giác
nên AM/MB=AD/DB=AM/MC(1)
Xét ΔAMC có ME là phân giác
nên AM/MC=AE/EC(2)
Từ (1) và (2) suy ra AD/DB=AE/EC
hay DE//BC

1: Xét ΔAMB có MD là phân giác
nên AD/DB=AM/MB=AM/MC(1)
Xét ΔAMC cso ME là phân giác
nên AE/EC=AM/MC(2)
Từ (1)và (2) suy ra AD/DB=AE/EC
hay DE//BC

Tam giác ABC có chu vi bằng 74cm, AC là cạnh lớn nhất. Đường phân giác của góc A chia cạnh BC thành hai đoạn tỉ lệ với 2:3; đường phân giác của góc C chia cạnh AB thành hai đoạn tỉ lệ với 4:5. Tính độ dài các cạnh của tam giác ABC.
AB + BC + AC = 74 (*)
Trong ∆ ABC phân giác AD → AB/AC = DB/DC = 2/3 (AC > AB)
→ AB = 2/3 . AC (1) , tương tự với phân giác CE ta suy ra
BC = 4/5 . AC (2) . Thế tất cả vào (*) ta được:
2/3 . AC + 4/5 . AC + AC = 74 → 37AC/15 = 74 → AC = 30cm
thế vào (1) và (2) ta được AB = 10cm, BC = 24cm

a: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔAMC có ME là phân giác
nên AE/EC=AM/MC
=>AD/DB=AE/EC
=>ED//BC
b: Xét ΔABM có DI//BM
nên DI/BM=AI/AM
Xét ΔACM có EI//MC
nên EI/CM=AI/AM
=>DI/BM=EI/CM
=>DI=EI

1: Xet ΔMAB co MD là phân giác
nen AD/DB=AM/MB=AM/MC
Xét ΔMCA có ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>DE//BC
2: Xét ΔABM có DG//BM
nên DG/BM=AG/AM
Xét ΔACM có EG//MC
nên EG/MC=AG/AM
=>DG/BM=EG/MC
mà BM=MC
nên DG=EG
=>G là trung điểm của DE
Để G là trung điểm của AM thì ADME là hình bình hành
=>DM//AC
=>D là trung điểm của AB
=>E là trung điểm của BC
=>AM/MB=AD/DB=1
=>AM=1/2BC
=>góc BAC=90 độ

1) AD phân giác góc A nên chia cạnh BC thành 2 đoạn tỉ lệ với 2 cạnh bên: ta có BD/DC = AB/AC
kẻ AH vuông góc BC tại H ta có S tam giác ABD = BD.AH/2 ; S tam giác ADC = DC.AH/2
VẬY S(ABD) / S(ACD) = ((BD.AH)/2) / ((CD.AH)/2) = BD/CD = AB/AC = m/n
mình làm nốt câu 2 vs câu 3 ở đây nha :))
Xét tam giác AMB có EM là phân giác :
\(\dfrac{EA}{EB}=\dfrac{AM}{BM}\)
Xét tam giác AMC có MD là phân giác :
\(\dfrac{AD}{DC}=\dfrac{AM}{MC}=\dfrac{AM}{BM}\) ( vì MB = MC )
\(\Rightarrow\) \(\dfrac{EA}{EB}=\dfrac{DA}{DC}\)
\(\Rightarrow\) DE // BC ( đpcm )
3) Ta có AE là đường phân giác của tam giác ABC nên ta có :
\(\dfrac{AE}{AB}=\dfrac{EC}{AC}\)
\(\)\(\dfrac{AE}{AB}=\dfrac{EC}{AC}=\dfrac{EB+EC}{AB+AC}=\dfrac{BC}{AB+AC}\)
\(\Rightarrow\) \(EB=\dfrac{AB.BC}{AB+AC}=\dfrac{5.7}{5+6}=\dfrac{35}{11}\left(cm\right)\)
\(\Rightarrow\) \(EB=BC-BE=7-\dfrac{35}{11}=\dfrac{42}{11}\left(cm\right)\)