Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(=x^2+7x-12x-84-2x+14\)
\(=x^2-7x-70\)
b)\(=x^2-4x-2x+8\)
\(=x\left(x-4\right)-2\left(x-4\right)\)
\(=\left(x-4\right)\left(x-2\right)\)
c) \(=9x\left(x+y\right)-\left(x+y\right)\)
\(=\left(9x-1\right)\left(x+y\right)\)
d)\(=\left(x-y\right)^2-9^2\)
\(=\left(x-y+9\right)\left(x-y-9\right)\)
e)\(=x^2+8x+16-60+15x\)
\(=x^2+23x-44\)

a) Áp dụng HĐT 1 thu được ( 2 x + y ) 2 .
b) Áp dụng HĐT 3 với A = 2x + l; B = x - l thu được
[(2x +1) + (x -1)] [(2x +1) - (x -1)] rút gọn thành 3x(x + 2).
c) Ta có: 9 - 6x + x 2 - y 2 = ( 3 - x ) 2 - y 2 = (3 - x - y)(3 -x + y).
d) Ta có: -(x + 2) + 3( x 2 - 4) = -{x + 2) + 3(x + 2)(x - 2)
= (x + 2) [-1 + 3(x - 2)] = (x + 2)(3x - 7).

Bài 3:
a: =>(2x-7)(x-2)=0
=>x=7/2 hoặc x=2
b: =>(x-1)(x+2)=0
=>x=1 hoặc x=-2
d: =>2x+3=0
hay x=-3/2

Câu 2:
a: \(\left(x-1\right)\left(x+1\right)-x\left(x+3\right)+7=0\)
=>\(x^2-1-x^2-3x+7=0\)
=>-3x+6=0
=>-3x=-6
=>\(x=\dfrac{-6}{-3}=2\)
b: \(2x^3-22x^2+36x=0\)
=>\(2x\left(x^2-11x+18\right)=0\)
=>\(x\left(x^2-11x+18\right)=0\)
=>\(x\left(x^2-2x-9x+18\right)=0\)
=>\(x\left[x\left(x-2\right)-9\left(x-2\right)\right]=0\)
=>\(x\left(x-2\right)\left(x-9\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-2=0\\x-9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=9\end{matrix}\right.\)
Câu 4:
1: Diện tích cỏ cần thay là:
\(105\cdot68=7140\left(m^2\right)\)
Số tiền BQL sân cần trả là:
\(7140\cdot120000=856800000\left(đồng\right)\)
2:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: Xét ΔADE có
H,M lần lượt là trung điểm của AE,AD
=>HM là đường trung bình của ΔADE
=>HM//DE
=>BC//DE
=>\(\widehat{EDB}=\widehat{DBM}\)(hai góc so le trong)(1)
Ta có: ABDC là hình chữ nhật
=>AD=BC
mà \(MD=\dfrac{AD}{2};MB=\dfrac{BC}{2}\)
nên MD=MB
=>ΔMBD cân tại M
=>\(\widehat{MDB}=\widehat{MBD}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MDB}=\widehat{EDB}\)
=>\(\widehat{ADB}=\widehat{EDB}\)
=>DB là phân giác của góc ADE

a) 3x2 – 7x + 2
\(=3x^2-6x-x+2\)
\(=\left(3x^2-6x\right)-\left(x-2\right)\)
\(=3x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(3x-1\right)\)
b) a(x2 + 1) – x(a2 + 1)
\(=ax^2+a-\left(a^2x+x\right)\)
\(=a\left(x^2+1\right)-x\left(a^2+1\right)\)
.......?
a) Ta có: \(3x^2-7x+2\)
\(=3x^2-6x-x+2\)
\(=3x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(3x-1\right)\)
b) Ta có: \(a\left(x^2+1\right)-x\left(a^2+1\right)\)
\(=x^2a+a-a^2x-x\)
\(=\left(x^2a-a^2x\right)+\left(a-x\right)\)
\(=xa\left(x-a\right)-\left(x-a\right)\)
\(=\left(x-a\right)\left(xa-1\right)\)
c) Ta có: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+120-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+96\)
\(=\left(x^2+7x\right)^2+16\left(x^2+7x\right)+6\left(x^2+7x\right)+96\)
\(=\left(x^2+7x\right)\left(x^2+7x+16\right)+6\left(x^2+7x+16\right)\)
\(=\left(x^2+7x+16\right)\left(x^2+7x+6\right)\)
\(=\left(x^2+7x+16\right)\left(x+1\right)\left(x+6\right)\)
d) Ta có: \(\left(a+1\right)\left(a+3\right)\left(a+5\right)\left(a+7\right)+15\)
\(=\left(a^2+8a+7\right)\left(a^2+8a+15\right)+15\)
\(=\left(a^2+8a\right)^2+22\left(a^2+8a\right)+105+15\)
\(=\left(a^2+8a\right)^2+22\left(a^2+8a\right)+120\)
\(=\left(a^2+8a\right)^2+12\left(a^2+8a\right)+10\left(a^2+8a\right)+120\)
\(=\left(a^2+8a\right)\left(a^2+8a+12\right)+10\left(a^2+8a+12\right)\)
\(=\left(a^2+8a+12\right)\left(a^2+8a+10\right)\)
\(=\left(a+2\right)\left(a+6\right)\left(a^2+8a+10\right)\)

a: =4(x-2)(x+1)+4(x-2)^2+(x+1)^2
=(2x-4)^2+2*(2x-4)(x+1)+(x+1)^2
=(2x-4+x+1)^2=(3x-3)^2=9(x-1)^2
b: =x^7(x^2-1)-x^5(x+1)+x^3(x+1)+(x^2-1)
=(x+1)[x^7(x-1)-x^5+x^3+x-1]
=(x+1)[x^7(x-1)-x^3(x-1)(x+1)+(x-1)]
=(x+1)(x-1)(x^7-x^4-x^3+1)
=(x+1)(x-1)(x^3-1)(x^4-1)
=(x+1)(x-1)^2*(x^2+x+1)(x^2+1)(x-1)(x+1)
=(x+1)^2*(x-1)^3*(x^2+1)(x^2+x+1)
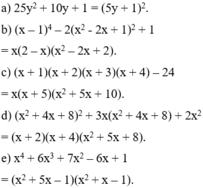
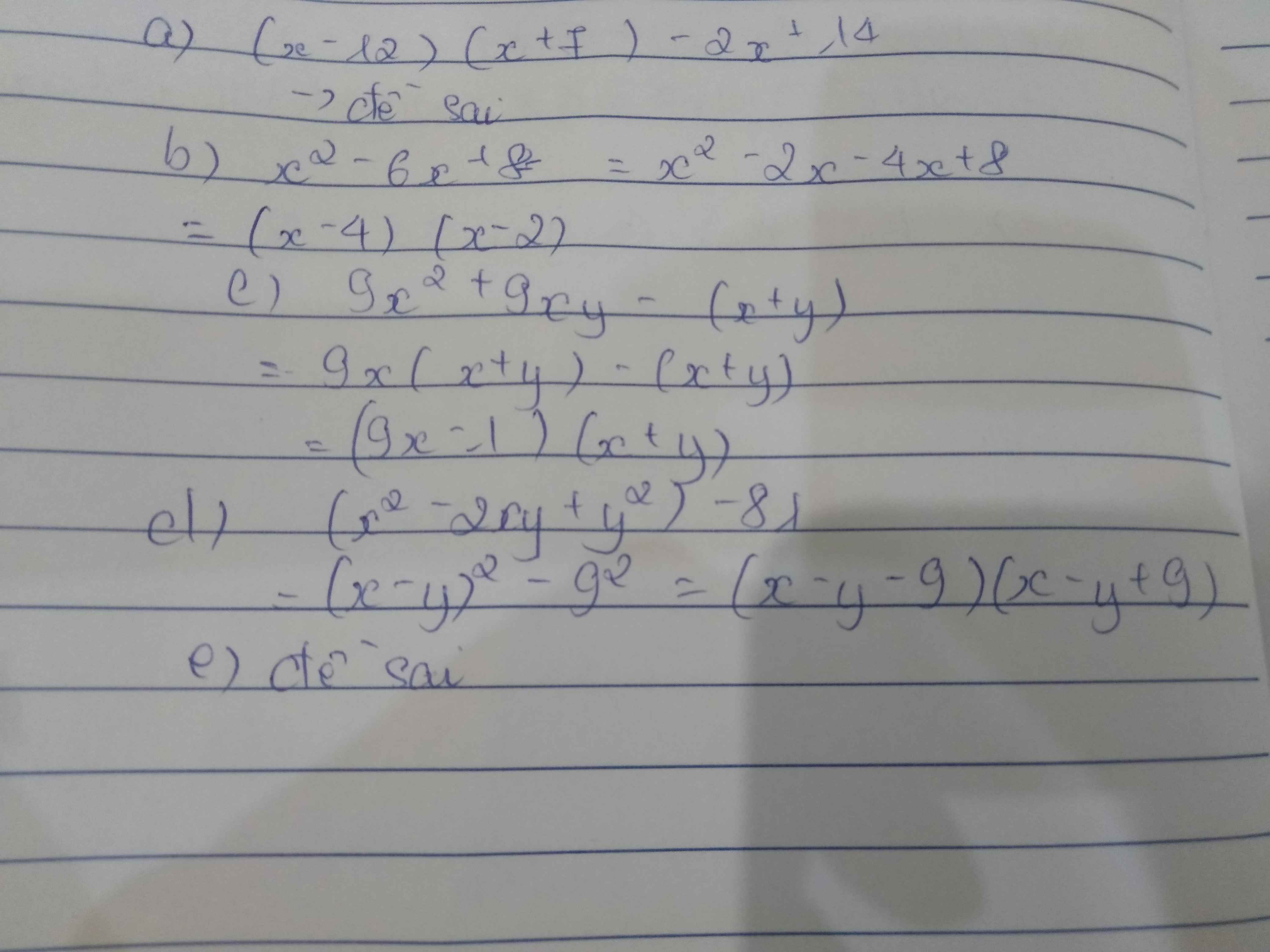
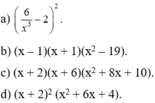
a) = x^2 - y^2 - x - y
= ( x- y)(x + y) - ( x+ y)
= ( x+ y)( x- y - 1 )
a)x2-x-y2-y
=x2-y2-x-y
=(x-y)(x+y)-(x+y)
=(x+y)(x-y-1)